Методът Монте Карло е
Случайните променливи се използват за решаване на различни приложни проблеми от дълго време. Пример за това е методът за определяне на числото пи, предложен от Буфон през 1777 г. Същността на метода е да се хвърли игла с дължинаLвърху равнина, начертана от успоредни линии, разположени на разстояниеrедна от друга (виж фиг. 1).
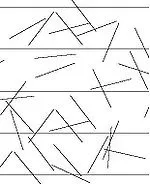
Вероятността (както може да се види от по-нататъшния контекст, ние не говорим за вероятност, а за математическото очакване на броя на пресичанията в едно преживяване; това става вероятност само при условие, чеr>L), че сегментът пресича линията, е свързана с числото Pi:
, Където
- A— разстояние от началото на иглата до най-близката до него права линия;
- θ е ъгълът на иглата спрямо правите линии.
Този интеграл е лесен за вземане: (при условие, чеr>L), така че като преброите дела на сегментите, които пресичат прави, можете приблизително да определите това число. С увеличаването на броя на опитите точността на резултата ще се увеличи.
През 1864 г. капитан Фокс, възстановявайки се от рана, за да се заеме по някакъв начин, реализира експеримент с хвърляне на игла. Резултатите са представени в следната таблица:
| 500 | 236 | 3 | 4 | отсъстващ | 3,1780 |
| 530 | 253 | 3 | 4 | настояще | 3,1423 |
| 590 | 939 | 5 | 2 | настояще | 3,1416 |
- Завъртането на самолета беше приложено (и, както показват резултатите, успешно), за да сеза намаляване на системната грешка.
- При третия опит дължината на иглата беше по-голяма от разстоянието между линиите, което направи възможно, без да се увеличава броят на хвърлянията, ефективно да се увеличи броят на събитията и да се подобри точността.
Връзка между стохастични процеси и диференциални уравнения
Създаването на математическия апарат на стохастичните методи започва в края на 19 век. През 1899 г. лорд Рейли показа, че едномерно произволно ходене по безкрайна решетка може да даде приблизително решение на параболично диференциално уравнение. Андрей Колмогоров през 1931 г. даде голям тласък на развитието на стохастични подходи за решаване на различни математически проблеми, тъй като той успя да докаже, че веригите на Марков са свързани с определени интегро-диференциални уравнения. През 1933 г. Иван Петровски показа, че случайна разходка, образуваща верига на Марков, е асимптотично свързана с решението на елиптично частично диференциално уравнение. След тези открития стана ясно, че стохастичните процеси могат да бъдат описани с диференциални уравнения и, съответно, изследвани с помощта на добре разработени математически методи за решаване на тези уравнения по това време.
Раждането на метода Монте Карло в Лос Аламос
Първо Енрико Ферми през 1930 г. в Италия, а след това Джон фон Нойман и Станислав Улам през 1940 г. в Лос Аламос, предполагат, че е възможно да се използва връзката между стохастичните процеси и диференциалните уравнения "в обратната посока". Те предложиха да се използва стохастичен подход за приближаване на многомерни интеграли в транспортните уравнения, възникнали във връзка с проблема за движението на неутрони в изотропна среда.
Идеята е разработена от Улам, който по ирония на съдбата също като Фокс се е борил с принудителното безделие.докато се възстановявах от болест и докато играех пасианс, се чудех каква е вероятността пасиансът да се "оправи". Той излезе с идеята, че вместо да използвате обичайната комбинаторика за подобни проблеми, можете просто да проведете „експеримента“ голям брой пъти и по този начин, преброявайки броя на успешните резултати, да оцените тяхната вероятност. Той също така предложи използването на компютри за изчисления на Монте Карло.
Появата на първите електронни компютри, които могат да генерират псевдослучайни числа с висока скорост, драстично разшири кръга от проблеми, за които стохастичният подход се оказа по-ефективен от другите математически методи. След това има голям пробив и методът Монте Карло се използва в много задачи, но използването му не винаги е оправдано поради големия брой изчисления, необходими за получаване на отговор с дадена точност.
По-нататъшно развитие и модерност
През 50-те години методът е използван за изчисления при разработването на водородната бомба. Основните заслуги в развитието на метода към този момент принадлежат на служителите на лабораториите на ВВС на САЩ и корпорацията RAND.
Монте Карло интеграция
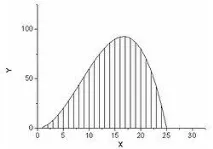
Да предположим, че трябва да вземем интеграла на някаква функция. Ще използваме неформално геометрично описание на интеграла и ще го разбираме като площта под графиката на тази функция.
За да определите тази област, можете да използвате един от обичайните числени методи за интегриране: разделете сегмента на подсегменти, изчислете площта под графиката на функцията на всеки от тях и добавете. Да предположим, че за функцията, показана на фигура 2, е достатъчно да се раздели на 25 сегмента и следователно да се изчислят 25 стойности на функцията. Представете си сегаимаме работа сn-мерна функция. След това имаме нужда от 25nсегмента и същия брой изчисления на стойността на функцията. Когато размерността на функцията е по-голяма от 10, задачата става огромна. Тъй като пространства с висока размерност се срещат, по-специално, в проблемите на теорията на струните, както и много други физически проблеми, където има системи с много степени на свобода, е необходимо да има метод за решаване, чиято изчислителна сложност няма да зависи толкова много от измерението. Това е свойство на метода Монте Карло.
Обикновен алгоритъм за интегриране на Монте Карло
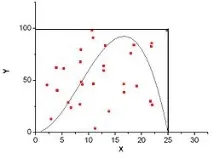
За да определите площта под графиката на функцията, можете да използвате следния стохастичен алгоритъм:
- ограничаване на функцията до правоъгълник (n-измерен паралелепипед в случай на много измерения), чиято площSparможе лесно да бъде изчислена;
- „хвърлете“ в този правоъгълник (паралелепипед) определен брой точки (Nчасти), чиито координати ще бъдат избрани на случаен принцип;
- определяне на броя на точките (Kчасти), които ще попаднат под графиката на функцията;
- площта на областта, ограничена от функцията и координатните оси,Sсе дава от следния израз
За малък брой измерения на интегрируемата функция производителността на интегрирането на Монте Карло е много по-ниска от производителността на детерминистичните методи. Въпреки това, в някои случаи, когато функцията е посочена имплицитно, но е необходимо да се определи областта, посочена под формата на сложни неравенства, стохастичният метод може да бъде по-предпочитан.
Използване на вземане на проби от значимост
Очевидно точността на изчисленията може да се увеличи, ако зоната, ограничаваща желаната функция, е възможно най-близо до нея. За това е необходимоизползвайте случайни променливи с разпределение, чиято форма е възможно най-близка до формата на интегрируемата функция. Това е в основата на един от методите за подобряване на конвергенцията в изчисленията Монте Карло: вземане на проби по значимост.
Оптимизация
Приложение във физиката
Компютърната симулация играе важна роля в съвременната физика и методът Монте Карло е един от най-разпространените в много области от квантовата физика до физиката на твърдото тяло, физиката на плазмата и астрофизиката.
Алгоритъм на Метрополис
Традиционно методът Монте Карло се използва за определяне на различни физически параметри на системи в термодинамично равновесие. Да предположим, че има наборW(S) от възможни състояния на физическата системаS. За да се определи средната стойност на някаква стойностA, е необходимо да се изчисли, където сумирането се извършва за всички състоянияSотW(S),P(S) е вероятността за състояниеS.
Динамична (кинетична) формула
Директна симулация на Монте Карло
Директната Монте Карло симулация на всеки физически процес включва моделиране на поведението на отделни елементарни части на физическа система. Всъщност тази директна симулация е близо до решаването на проблема от първи принципи, но обикновено се допускат някои физически приближения, за да се ускорят изчисленията. Като пример могат да служат изчисленията на различни процеси с помощта на метода на молекулярната динамика: от една страна, системата се описва чрез поведението на нейните елементарни компоненти, от друга страна, използваният потенциал за взаимодействие често е емпиричен.
Примери за директна симулация Монте Карло:
- Моделиранеоблъчване на твърди тела от йони в приближението на двойни сблъсъци.
- Директна Монте Карло симулация на разредени газове.
- Повечето от кинетичните модели на Монте Карло са директни (по-специално изследването на епитаксията на молекулярния лъч).
Квантов метод Монте Карло
Квантовият метод Монте Карло се използва широко за изследване на сложни молекули и твърди вещества. Това име съчетава няколко различни метода. Първият от тях е вариационният метод на Монте Карло, който по същество представлява числено интегриране на многомерни интеграли, които възникват при решаването на уравнението на Шрьодингер. За решаване на проблем, включващ 1000 електрона, са необходими 3000-измерни интеграли и при решаването на такива проблеми методът Монте Карло има огромно предимство в производителността пред други методи за числено интегриране. Друга разновидност на метода Монте Карло е дифузионният метод Монте Карло, който обаче не е много рационален.
Фондация Уикимедия. 2010 г.
Вижте какво е "методът Монте Карло" в други речници:
МЕТОД МОНТЕ КАРЛО — (метод на статистически тестове) числен метод за решаване на разкл. задачи чрез моделиране на случайни събития. В приложението към физиката М. К. м. може да се определи като метод за изучаване на физич. процес чрез създаване и опериране на стохастични. модели ... Физическа енциклопедия
МЕТОДЪТ МОНТЕ КАРЛО е метод за статистическо тестване, числен метод, базиран на моделиране на случайни променливи и конструиране на статистически данни. разчети за необходимите количества. Общоприето е, че M. K. m. възниква през 1949 г. (виж [1]), когато във връзка с работата по създаването на атомни ... Математическа енциклопедия
Метод Монте Карло - статистически метод за изпитване,числен метод за решаване на математически проблеми чрез моделиране (виж Моделиране) на случайни процеси и събития. Терминът „М. К. м." възниква през 1949 г., въпреки че някои изчисления са направени чрез моделиране на случайни ... Велика съветска енциклопедия
Монте Карло (метод) - Методът Монте Карло (методи на Монте Карло, MMK) е общото наименование на група числени методи, базирани на получаване на голям брой изпълнения на стохастичен (случаен) процес, който се формира по такъв начин, че неговите вероятностни ... ... Wikipedia
Метод Монте Карло — — [http://www.iks media.ru/glossary/index.html?gloss >Ръководство за технически преводач
МЕТОДЪТ МОНТЕ КАРЛО е метод за статистическо тестване, който се състои в решаване на изчислителна математическа задача чрез конструиране на случаен процес за нея с параметри, равни на желаните стойности на тази задача. Пример: изчисляваме M. M. K. 0 ≤ f (x) ≤1, при 0 ... ... Геологическа енциклопедия
Директна статистическа симулация Монте Карло — Директна статистическа симулация Монте Карло (Директна статистическа симулация Монте Карло) е изчислителен метод за газова динамика, предназначен за решаване на проблеми с динамиката на разредения газ. Методът може да се тълкува като решение на уравнението на Болцман. ... ... Wikipedia
МЕТОД МОНТЕ КАРЛО метод, Монте Карло; Немски Метод Монте Карло. Числен метод, основан на получаване на голям брой изпълнения на случаен процес, който се формира по такъв начин, че вероятностните характеристики да са равни на стойностите на проблема, който се решава. виж ... ... Енциклопедия по социология
Техника Монте Карло - [Техниката Монте Карло] (статистическо тестване) е един от методите за статистическо моделиране, базиран на кибернетичната идея за "черна кутия". Прилага се вв случаите, когато изграждането на аналитичен модел на явление е трудно ... ... Икономико-математически речник