Мистерията на геометрията на пирамидите ... в египетския триъгълник и в златното сечение

В чертежа начертайте права линия с произволна дължина и я разделете наполовина. Но за по-голяма яснота ще използваме същите цифрови изрази, които са налични в египетския триъгълник: 3, 4, 5. Като начален сегмент (фиг. 1) ще изобразим сегмента AB, чиято дължина ще бъде взета равна на 3 + 5 = 8, и нека да видим в какво съотношение ще бъде разделена на геометрични конструкции. Като начало разделяме сегмента AB наполовина: AD \u003d DV \u003d 4. Сега от края B на сегмента AB възстановяваме перпендикуляра OB, равен на половината от дължината на AB. Тоест OB \u003d AD \u003d DV \u003d 4. След това от точка O начертаваме окръжност с радиус OB и свързваме точки A и O с права линия. Пресечната точка на тази линия с окръжността ще бъде означена с точка C, след което нарисуваме дъга от окръжност през нея, чийто радиус е равен на AC. Дъгата ще раздели отсечката AB на две неравни части, които са в отношение AK : VK = 1,618. Всичко е в пълно съответствие със златното сечение. Проблема решен? Да, сегментът е разделен в правилното съотношение.
Но задачата има продължение, което е най-пряко свързано с египетския триъгълник и някои тайни на пирамидите.
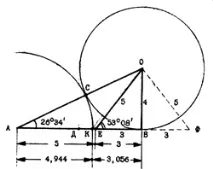
Фиг.1. При разделяне на сегмента AB \u003d 8 в екстремно и средно съотношение, желаната точка K разделя сегмента AB на две части: AK \u003d 4,944 и BK \u003d 3,056. В този случай AB:AK=8:4.944 = 1.618 и AK:VK = 4.944:3.056 = 1.618. Полученото по този начин число 1,618 се нарича златно сечение, а процесът на разделяне на сегмента в крайно и средно съотношение се нарича златно сечение. В древен Египет е използван друг метод за разделяне на отсечката AB = 8, много близък до златното сечение.Желаната точка E разделя отсечката AB на две части в съотношение 5:3. В този случай AE = 5 и BE = 3. В този случай AB:AE = 8:5 = 1,6 и AE:BE = 5:3 = 1,666. Този метод направи възможно да се изразят законите на златното сечение с помощта на цели числа.числа на "египетския" правоъгълен триъгълник OBE със съотношение на страните 3:4:5. Той беше много удобен за практическо използване и беше нещо като стандарт в Египет. Съотношенията OB: AB, образувани при това разделяне на сегмента, са 1: 2. OB:EF = 2:3, BE:OB:OE: - 3:4:5, както и ъгли 26°34′ и 53°08′ са положени при проектиране, маркиране и строителни работи при изграждането на пирамиди и други конструкции. Равнобедреният триъгълник OEF беше част от пирамида, прекарана през средината на две противоположни стени. Такава пирамида отговаряше на изискванията на "египетския" триъгълник, а на практика - на златното сечение с приемлива точност. Ъгъл 26°34′, равен на половината от ъгъл 53°08′. използван е главно при изграждането на наклонени галерии, стълбища, коридори... Такъв наклон има например коридорът на пирамидата на Хеопс (фиг. 2).
Ако свържем точките O и E с права линия, получаваме правоъгълен египетски триъгълник EOB със съотношение на страните BE: BO: EO = 3:4:5. Кой би предположил, че се крие на такова място! Че невидимо присъства при разделянето на сегмент в средни и крайни съотношения! Че е дете на златното сечение и като че ли му е роднина! С една дума там. къде е египетският триъгълник - търсете златното сечение. И обратното: след като сте забелязали златното сечение, потърсете египетския триъгълник наблизо.
В триъгълник EOB ъгълът OEB е 53°08′. Лесно е да се изчисли чрез тангенса: OB: EB = 4: 3 = 1,333. Ъгълът 53°08′ е най-пряко свързан с пирамидите на Хеопс. Хефрен, Микерин. И на повечето други пирамиди в Египет. Например в пирамидата на Хефрен ъгълът на наклона на лицето към основата е почти равен на ъгъла на египетския триъгълник. Ъгълът на наклона на страничните стени на пирамидите на Хеопс и Менкаур е близък до теоретичния. Разликата е само една или две степени. Оказва сече пирамидите са построени с очакването да изпълнят възможно най-точно условията на златното сечение. Не е изненадващо, че пирамидите в Гиза все още не са се срутили.
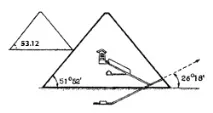
Фиг.2. В пирамидата на Хеопс (вдясно) ъглите на наклона на лицата и входния коридор са близки до ъглите на триъгълниците, образувани при разделянето на сегмента в средно и крайно съотношение (фиг. 1). А в пирамидата на Хефрен (вляво) ъгълът на наклона на лицата е почти равен на ъгъла от 53 ° 08 ′. Грешката е само четири минути
Геометричната конструкция, показана на фиг. 1 крие още една тайна, свързана с пирамидите. Той е „скрит“ в правоъгълния триъгълник AOB. По-скоро в големината на ъгъла OAB. Може да се изчисли с помощта на тангенса: RH: AB = 4:8 = 0,5. Тангенса 0,5 съответства на ъгъл от 26°34′. И тук се оказва, че той е равен на половината от ъгъла OEV: 53°08′: 2 = 26°34′. Ако сега сравним големината на този ъгъл с ъгъла на наклона на коридора, водещ вътре в пирамидата на Хеопс, няма да видим съществена разлика! (фиг. 2). Нека погледнем този триъгълник AOB отново от малко по-различен ъгъл. В него OB: AB \u003d 4:8 \u003d 1:2. Отново съотношението на златната серия! Така че, когато разделихме сегмента в средното и крайното съотношение, получихме цяла поредица от числа, пряко или косвено свързани със златното сечение: 1,618; 1:2, 2:3, 3:4:5. Ето го египетския триъгълник! Оказва се, че това е само основната връзка в дълга верига от взаимосвързани знания, хващайки се за която можете последователно да извадите всички останали. Нищо чудно, че очевидно трябваше да прекараме толкова много време на „моста на магаретата“, за да разберем цялата философия на Вселената с помощта на египетския триъгълник, да отгатнем принципите, които са в основата на създаването на природата. Но повече за това в други глави.