Многовариантна безградиентна оптимизация
Многоизмерна оптимизация. Концепцията за методите.
Математическата формулировка на задачата има следния вид:
Нека формулираме проблема с условната оптимизация в традиционната форма:
Намерете минимума на целевата функция
(1)
чрез променливи за търсене при наличие на различни ограничения:
за променливи за търсене
, (2)
l=1,L; L-брой променливи за търсене;
върху променливи за търсене под формата на функционални неравенства, (3)
j=1,J; J е броят на функционалните неравенства;
за търсене на променливи под формата на функционални равенства , (4)
i=1,I. I - брой функционални равенства.
В този раздел се разглеждат числени методи за оптимизация, при които размерът и посоката на стъпката към оптимума се формират еднозначно от определени детерминистични функции в зависимост от свойствата на критерия за оптималност в близост до текущата точка, без да се използват производни (т.е. градиент). Всички алгоритми са итеративни по природа и за променливата i на j +1 итерациите се изразяват с формулата:
. (5)
За разглежданата група методи . Сред тези методи се отличават: методът на Gauss-Seidel, методът на Hook-Jeeves, методите на деформируемите полиедри (методът на симплекса). Основната характеристика на разглежданата група методи е липсата на изчисляване на градиента на критерия за оптималност. Редица методи за директно търсене се основават на последователното прилагане на едномерно търсене в променливи или в други определени посоки, което улеснява тяхното алгоритмизиране и приложение.
3.5. Метод на координатно спускане
Един от методите за намиране на минимума на функция от n-променливи са методите за директно търсене. Методите за директно търсене са методи, които използват само функционални стойности. Същността на метода еалтернативна едномерна оптимизация на целевата функция с помощта на едномерни методи за оптимизация, например използване на метода на златното сечение за всяка променлива X1, ..., Xn на свой ред.
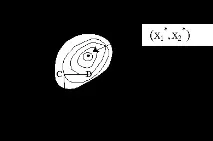
Да разгледаме функция на две променливи. Линиите му на ниво са показани на фиг.1, а минимумът е в точката (x1 * ,x2 * ). Най-простият метод за търсене еметодът на спускане по координати. От точка A ще търсим минимум по посока на оста x1 и по този начин ще намерим точката B, в която допирателната към линията на постоянно ниво е успоредна на оста x1. След това, търсейки от точка B по посока на оста x2, получаваме точка C, търсейки успоредно на оста x2, получаваме точка D и т.н. Така стигаме до оптималната точка. Очевидно тази идея може да се приложи към функция от n променливи. Теоретично този метод е ефективен в случай на единичен минимум на функцията. Но на практика се оказва твърде бавен. Поради това са разработени по-сложни методи, които използват повече информация въз основа на вече получени стойности на функцията.
3.6. Метод на симплексна оптимизация.
Симплексът е правилен полиедър с n + 1 върха, където n е броят на факторите, влияещи върху процеса. Така например, ако има два фактора, тогава правилният триъгълник е симплекс.
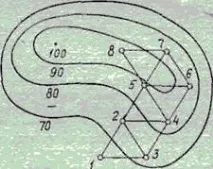
Фиг.2. Оптимизация по симплексния метод
Същността на симплексния метод за оптимизация е илюстрирана на фиг. 2. Първоначалната серия от експерименти съответства на върховете на оригиналния симплекс (точки 1, 2 и 3). Условията на тези първи експерименти са взети от диапазона от стойности на факторите, съответстващи на най-благоприятния от известните режими на процеса, който се оптимизира. Сравнявайки резултатите от експериментите в точки 1, 2 и 3, те намират сред тях „най-лошия“, сот гледна точка на избрания критерий за оптималност. Нека например експериментът в точка 1 се окаже най-„неуспешен". Този експеримент се изключва от разглеждане и вместо това в симплекса се въвежда експериментът в точка 4, който е симетричен на точка 1 спрямо противоположната страна на триъгълника, свързващ точки 2 и 3. След това се сравняват резултатите от експериментите във върховете на новия симплекс, като най-„неуспешният" от тях се отхвърля и съответният връх на симплекса се прехвърля в точка 5. След това разглежданата процедура се повтаря през целия процес на оптимизация. Ако се достигне екстремумът на критерия за оптималност, по-нататъшното движение на симплекса спира. Това означава, че новата стъпка връща изследователя към предишната точка във факторното пространство. Трябва да се отбележи, че симплексът
методът, както и другите методи за оптимизация, е локален метод за търсене на екстремуми. Ако има няколко екстремума на критерия за оптималност, тогава този метод позволява да се намери този, който е по-близо до точките на оригиналния симплекс. Следователно, ако има подозрение за съществуването на няколко екстремума на критерия за оптималност, е необходимо да ги търсите, като всеки път започвате оптимизация от нов регион на факторното пространство. След това трябва да сравните намерените оптимални условия помежду си и да изберете най-доброто от всички опции.
3.7 ТЪРСЕНЕ ВЪРХУ ДЕФОРМИРУЕМ МНОГОСТЪР
симплексен метод (да не се бърка със симплексния метод в линейното програмиране). Той е по-прост, но се използва широко при решаване на задачи за планиране на екстремни експерименти.
Ориз. 3. Илюстрация на идеята за симплексния метод
Симплексите се наричат правилни полиедри. Например, за случая на две променливи това ще бъде равностранен триъгълник, за трипроменливи - тетраедър и др. Тестовите точки (фиг. 3) съвпадат с върховете на симплекса (точки 1, 2, 3). От върха, в който целевата функция е максимална (точка 1), се изчертава издадена права линия през центъра на тежестта на симплекса. След това се изгражда нов симплекс, наречен отразен, от точки 2, 3 и нова точка 4, разположени на проектиращата права на съответното разстояние от центъра на тежестта. Тази процедура, при която всеки път, когато върхът с максималната целева функция се зачертава, се повтаря. Триъгълникът (в случай на две променливи) е, така да се каже, обърнат към страната с най-малките стойности на целевата функция. Има правила за постепенно намаляване на размера на симплекса и за предотвратяване на циклично движение в близост до минимума. Използването на правилни полиедри причинява редица недостатъци на метода: неефективно търсене в извити дерета, забавяне на търсенето в някои ситуации. При метода на деформируем полиедър симплексът може да промени формата си, така че е по-добре да се адаптира към характеристиките на многоизмерната повърхност. Нека обозначим координатите на върховете на многостена при c-та стъпка
Хi,k i = 1, . . ., n + 1; k = 0, 1, . Избираме върховете, при които целевата функция е максимална и минимална, и ги обозначаваме съответно с Xbad (Xmax) и Xgood(Xmin). (за да опростим формулите, ще пропуснем индекса на стъпка k в това, което следва) Означете с X центъра центъра на тежестта на всички върхове, с изключение на Xbad:
Xn+2,j=
Работата на метода се състои от следните операции: отражение, разтягане, компресия и редукция (фиг. 4).
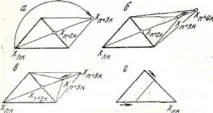
Ориз. 4. Операции на метода на деформируемия многостен
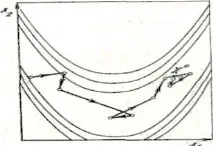
Ориз. 5. Траектория на метода на деформируемите полиедри.