Описание на докладите за решението на проблема - Studiopedia
Отчет за резултатите: таблицаЦелева клетка показва информация за целевата функция; таблицаПроменяеми клетки показва стойността на необходимите променливи, получени в резултат на решаването на проблема; таблицаОграничения показва резултатите от оптималното решение за ограничения и за гранични условия. В полетоФормула са дадени зависимости, въведени в прозорецаТърсене на решение, в полетоРазлика - стойностите на използвания материал. Ако материалът е напълно използван, тогава полетоСтатус показваобвързан, ако материалът не е напълно използван, това поле показване е обвързан. За гранични условия се дават подобни стойности с единствената разлика, че вместо стойността на неизползвания продукт се показва разликата между стойността на променливата в намереното оптимално решение и граничното условие, определено за него.
Докладът за стабилност съдържа информация за това колко стабилно е полученото решение с промени в коефициентите на целевата функция и ограниченията. КолонатаПроменяеми клетки съдържа изчислените стойности на необходимите променливи и техните двойни оценки. За всяка променлива се изчислява показателятНормална цена (в Excel 7.0 - "намалена цена") - коефициент, показващ колко се променя целевата функция, когато съответната променлива се промени (т.е. когато е принудена да бъде включена в оптималния план) с единица. В същата колона са дадени оценки за пределните увеличения на коефициентите на целевата функция (допустимо увеличение и допустимо намаление), при които е възможно правилното прилагане на показателя „нормализирани разходи“, а също така се запазва оптималното решение (т.е. структурата на оптималнияплан).
КолонатаОграничения съдържа подобни стойности и двойни оценки за ограниченията на проблема за оптимизация.Shadow price е коефициент, показващ колко се променя целевата функция, когато съответният ресурс (ограничение) се промени с единица. КолонитеДопустимо увеличение иДопустимо намаление показват граничните стойности на увеличенията на ресурсите, при които се запазва номенклатурата на оптималния план (променливите, включени в основата, остават) и индикаторът „цена в сянка“ може да се приложи правилно.
Отчет по граници – отчетът показва границите, в които може да се променя количеството на материалите, включени в оптималното решение, като същевременно се запазва структурата на оптималното решение; дадени са стойностите на променливите в оптималното решение, както и долната и горната граница на изменението на стойностите на променливите; също така показва стойностите на целевата функция за освобождаване на този вид продукт на горната и долната граница.
3. Двойственост в задачите на линейното програмиране. Анализ на получените оптимални решения
През 1975 г. нашият сънародник Л.В. Канторович е удостоен с Нобелова награда по икономика (заедно с американския икономист Т. Купманс) за разработването на теорията за оптималното използване на ресурсите. Тясно свързан с всеки проблем на линейното програмиране е друг линеен проблем, наречен двоен; първоначалният проблем се наричаоригинален,илидиректен.Връзката между оригиналния и двойния проблем се състои по-специално във факта, че решението на единия от тях може да бъде получено директно от решението на другия.
Променливите на двойната задачаyiсе наричат обективно определени оценки(или двойни оценки, "цени" на ресурсите, цени в сянка).
Всеки отПроблемът с двойната двойка всъщност е независим проблем за линейно програмиране и може да бъде решен независимо от другия.
Двойният проблем по отношение на оригиналния се съставя съгласно следните правила:
1) целевата функция на първоначалния проблем е формулирана за максимума, а целевата функция на двойния проблем е формулирана за минимума, докато в максималния проблем всички неравенства във функционалните ограничения имат формата (≤), в минималния проблем формата (≥);
2) матрицаA,, съставена от коефициенти при неизвестни ограничения в оригиналната проблемна система, и подобна матрицаA T в двойния проблем се получават една от друга чрез транспониране;
3) броят на променливите в двойния проблем е равен на броя на функционалните ограничения на първоначалния проблем, а броят на ограниченията в системата на двойния проблем е равен на броя на променливите в оригиналния проблем;
4) коефициентите за неизвестни в целевата функция на двойствения проблем са свободни членове в системата от ограничения на оригиналния проблем, а десните страни в ограниченията на двойния проблем са коефициентите за неизвестни в целевата функция на оригинала;
5) всяко ограничение на една задача съответства на променлива на друга задача, номерът на променливата съвпада с номера на ограничението. В този случай ограничението, записано като неравенството ≤, съответства на променлива, ограничена от условието за неотрицателност. Ако функционалното ограничение на първоначалния проблем е равенството, тогава съответната променлива на двойния проблем може да приеме както положителни, така и отрицателни стойности.
Моделът на първоначалния (директен) проблем в общ вид може да бъде написан по следния начин:
, (10)
(единадесет)
а моделът на двойствения проблем е
(12)
(13)
Решаване на LLP симплекс-метод, ние едновременно решаваме двойния LLP. Променливите на двойствения проблемyί се наричат обективно определени оценки.
Обмислете анализа на оптималното решение въз основа на пример 1. Решението е направено с помощта на MS Excel (Търсене на решение ) и е показано на фигура 13.
Създаване на отчет за резултатите от намирането на решение
Excel ви позволява да представите резултатите от търсенето на решение под формата на отчет (фиг. 25, 26).
Има три вида такива отчети:
- отчет за устойчивост "Чувствителност", съдържащ информация за чувствителността на решението към малки промени в променящите се клетки или във формулите за ограничения;
- отчет за ограниченията „Ограничения“. В допълнение към изходните и крайните стойности на променливите и целевите клетки, отчетът включва горната и долната граница на стойностите, които влияещите клетки могат да приемат, при спазване на ограниченията;
- отчет за резултатите „Отговор“. Докладът включва изходните и крайните стойности на целевите и модифицираните клетки, допълнителна информация за ограниченията.
Отчетът за резултатите съдържа оптималните стойности на променливитеX1, X2, X3, X4, които съответно са равни на 0; тридесет; 10; 0; стойността на целевата функция е 150, както и левите части на ограниченията (фиг. 25).
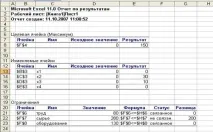
Ориз. 25. Отчет за резултатите
Не намерихте това, което търсихте? Използвайте търсачката:
Деактивирайте adBlock! и обновете страницата (F5)наистина е необходимо