Откъде идва усмивката на непостоянството

Продължавайки вече популярната тема с моделите на усмивка за волатилност, искам да споделя резултатите от моите изследвания по тази тема. Малко е тъпо да се прави това след поста на Виталий Курбаковски. Но може би някой и моите изследвания ще бъдат интересни. Аз самият не съм математик или търговец, просто програмист. Затова не съдете строго.

Наблюдавайки поведението на усмивката на нестабилност, въпросите отдавна са измъчвани от: Защо усмивката се издига нагоре и надолу? Защо е извит така, а не иначе? Защо BA се преобръща към текущата цена, а долната част на усмивката е вдясно от BA и само при изтичане се изтегля до BA и усмивката става симетрична? Защо клоните й вървят нагоре-надолу? И големият въпрос е: Какво причинява усмивката на нестабилност? Някои източници твърдят, че усмивката се дължи на дебелите опашки на разпределението на нарастванията. Реших да го проверя и да направя някои изследвания.

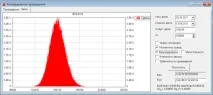
Доколкото разбирам теорията на въпроса, за да изчислите усмивката си за волатилност, трябва да имате вероятностно разпределение за това каква ще бъде цената на BA за изтичане (наричано по-долу - разпределение на цените). Ако знаете това разпределение, тогава можете недвусмислено да изчислите цените на опциите при всяка стачка и след това, като използвате формулата на Блек-Шоулс, можете да изчислите IV при всяка стачка и да получите усмивка за волатилност. Как мога да получа разпределението на цените? Реших да го изградя, като генерирам хиляди произволни ценови траектории, започвайки от текущата стойност на BA. Запазвам крайните точки на траекториите (BA цена за изтичане) и накрая гледам колко често цената попада в един или друг диапазон. Ето как получавам разпределението на цените за изтичане. За да изградя произволна траектория, реших да използвам разпределението на нарастванията, които действително съществуват на пазара (наричано по-долу емпирично разпределение). Тук,например разпределение на инкрементите (в минути) за RTS-9.11 фючърси:

Графика на нормална плътност на разпределение е насложена върху хистограмата на разпределението на реалните инкременти. Вижда се, че разпределението на реалните прирасти се различава от нормалното:

Вероятността от незначителни промени в цената е по-голяма, отколкото при нормалното разпределение;
Вероятността за промяна на средната цена е по-малка от нормалната;
Вероятността от значителни промени в цените е по-голяма, отколкото при нормалното (площта под опашките + -3 * сигма на емпиричното разпределение е три пъти по-голяма от тази на нормалното разпределение);

Може би усмивката на волатилността възниква точно поради тези разлики между емпиричното разпределение и нормалното? Нека да го проверим. Нека изградим разпределението на цените за изтичане, използвайки емпиричното разпределение. Но първо, нека го променим малко. Работата е там, че емпиричното разпределение вече съдържа тенденцията, която BA имаше за разглеждания период (например RTS-9.11 падна от 183505 на 161190 за избрания период). И ако използваме първоначалното емпирично разпределение, тогава очакването на разпределението на цените за изтичане ще бъде много различно от началната точка на траекториите. Невъзможно е да се изгради усмивка на волатилност върху такова разпределение. Тъй като паритетът на повикване няма да бъде извършен. И усмивките, изчислени отделно за путове и колове, няма да съвпадат. За да се изпълни паритетът, е необходимо очакването на разпределението на цените за изтичане да е равно на текущата цена на BA (началната стойност за всички траектории). Нека изключим компонента на тенденцията от увеличенията (както broker25 съветва в тази публикация) и начертайте коригираното разпределение на цените при изтичане:

Това разпределение има същото очакване като текущата стойност на BA, така че усмивките могат да бъдат изчислени. Да преброимусмивка отделно за поставяне и отделно за обаждания. Ето какво се случи:

Дебелата черна линия е усмивката на променливостта, която борсата излъчваше по това време. Зеленото е усмивката на волатилността, изчислена от разпределението на цената за кол опциите. Розовото е усмивката на волатилността за пут опциите.

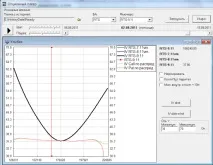
Вижда се, че изчислените усмивки започват да се разминават по краищата, т.е. паритетът на call-put престава да се изпълнява. Но най-важното е, че изчислените усмивки изобщо не са като парабола. И приличат повече на хоризонтална линия. Как обменната усмивка получава парабола?

Тук се борих дълго време, проверявайки отново изчисленията, но всички изяснения доведоха до факта, че усмивката ставаше все повече и повече като хоризонтална линия. Все още не съм забелязал, че в теоретичните цени, излъчвани от борсата, минималната присъща стойност на опция никога не е по-малка от 10p. След като въведох такава корекция, получих тази усмивка:

Това вече прилича повече на борсова усмивка. Но все пак частично линейната структура обърква. Нека премахнем корекцията от 10p и изкуствено „претеглим“ опашките на ценовото разпределение, така че това условие (присъща цена на опцията >= 10p) да се изпълни автоматично. За такова разпределение получаваме следната усмивка:

Изглежда, че сме на прав път и усмивката е все по-близо до размяната. Единственият въпрос е как точно да се "претеглят" опашките на ценовото разпределение? И защо точно те трябва да бъдат "претеглени"? В края на краищата ние използвахме разпределението на стъпките, в които опашките вече бяха много по-дебели от тези на нормалното разпределение. Може би причината се крие в зависимостта на приращенията. Когато изградихме следващата произволна траектория на движението на BA до изтичане, тогава на всяка стъпка следващото увеличение беше избрано независимо от предишното. Тези. изхождахме от принципа, че нарастванията в емпиричното разпределение са независими. Нонаистина ли е

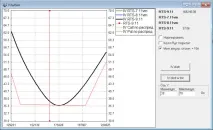
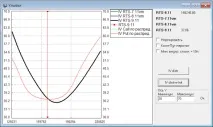
Нека проведем експеримент: след всяко значително увеличение (например с + 100p), ще запомним следващото увеличение и ще видим какво ще се окаже разпределението на тези увеличения. Ето условното разпределение:

Може да се види, че очакването на това разпределение не е нула (0,02% от цената на BA) и 60% от увеличенията са положителни. Тези. в 60% от случаите, след покачване със 100p или повече, на следващия бар движението нагоре продължава и средно е около 30-40p (забележка за скалперите!). Тези. нашият експресен анализ показва, че инкрементите не могат да се считат за независими. И за да генерирате произволна траектория на движение на цената, трябва не просто произволно да изберете следващото увеличение, но да използвате някои зависимости.

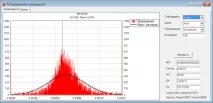
Нека се опитаме да симулираме такива зависимости. Например, разгледайте този вариант: в 98% от траекториите са построени абсолютно случайно, в 1% траекторията е построена произволно, но с тенденция към спад, в 1% - към растеж. Ето разпределението на цените:

При такова разпределение се получава следната усмивка на волатилност:

Формата на усмивката се доближава до борсовата. Нека сега се заемем с дъното на усмивката. Долната част на усмивката, излъчена от борсата, е вдясно от текущата стойност на BA и когато наближи изтичането, тя се издига до BA. И в последния ден усмивката най-накрая става симетрична. Каква е причината за това поведение на усмивка? Олег Мубаракшин помогна тук:

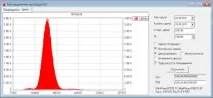
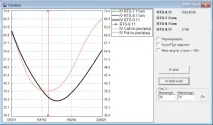
Корелацията между цената и волатилността е отговорна за изместването на дъното. Това, което наблюдаваме при опциите на индекса, е следствие от отрицателната корелация между увеличенията в цената на фючърса и увеличенията в неговата волатилност. Нека се опитаме да симулираме това. Тези. ще използваме не фиксирано разпределение на стъпките, а динамично променящо се, вв зависимост от това дали текущата ценова траектория расте или пада. Ако расте, постепенно ще намалим волатилността. Ако падне, ще вдигнем воля. Ето разпределението на цените, получено с тази симулация:

Може да се види, че сега лявата страна на разпределението е по-разтегната, тъй като за изграждането му е използвано по-променливо разпределение на инкрементите. Сега нека да разгледаме усмивката, която се получава с това разпределение на цените:

Усмивката отдясно има леко извиване, очевидно ценовото разпределение отдясно не е имало достатъчно дебела опашка. Но най-важното е, че изявлението на Олег се потвърди! Дъното наистина се измести надясно. Ако погледнете динамиката, тогава дъното на такава усмивка ще бъде същото като това на обменната усмивка, тъй като наближава изтичането, тя ще се изтегли до BA.

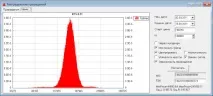
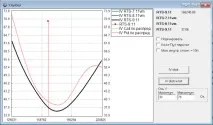
И така, ето отговорите на първоначалните въпроси:

Разликата между емпиричното разпределение на нарастванията и нормалното разпределение и неговите дебели опашки не е причината за усмивката.
Усмивката идва от тлъстите опашки на разпределението на изтичащите цени.
Най-вероятно тези мастни опашки възникват поради зависимостта на нарастванията в емпиричното разпределение.
Вертикалната позиция на усмивката зависи от сигмата на разпределението на инкремента: разпределение с по-висока сигма ще повдигне усмивката вертикално нагоре, с по-малко ще я спусне надолу.
Наклонът на клона на усмивката зависи от „тежестта“ на опашката на ценовото разпределение: колкото „по-тежка“ е опашката, толкова по-голям е ъгълът на наклона на съответния клон на усмивката.
Изместването на долната част на усмивката надясно е свързано с отрицателна корелация между цената на BA и нейната волатилност.

Ето изследване и такива изводи. Ще се радвам на всякаква критика или нови идеи.