ПИТАГОРОВАТА ТЕОРЕМА - Студиопедия
Трудно е да се намери човек, който да не свързва името Питагор с Питагоровата теорема. Може би дори тези, които в живота си се сбогуваха с математиката завинаги, запазват спомени за „Питагоровите панталони“ - квадрат на хипотенузата, равен по размер на два квадрата на краката. Причината за такава популярност на Питагоровата теорема е триединна: това е простота - красота - значимост. Наистина, Питагоровата теорема е проста, но не е очевидна. Тази комбинация от две противоречиви начала й придава особена привлекателност, прави я красива. Но освен това теоремата на Питагор е от голямо значение: тя се използва в геометрията буквално на всяка стъпка и фактът, че има около 500 различни доказателства за тази теорема (геометрични, алгебрични, механични и т.н.), показва гигантски брой нейни специфични реализации.
И така, оптимистът Михайло Ломоносов (1711 - 1765) пише: „Питагор пожертва сто вола на Зевс за изобретяването на едно геометрично правило. Но ако правилата, открити в съвременните времена от остроумни математици, действат според неговата суеверна ревност, тогава едва ли би било възможно да се намерят толкова много добитък в целия свят.
Но ироничният Хайнрих Хайне (1797-1856) вижда развитието на същата ситуация малко по-различно: „Кой знае! Кой знае! Може би душата на Питагор се е преместила в бедния кандидат, който не можа да докаже Питагоровата теорема и се провали поради това на изпитите, докато неговите изпитващи са обитавани от душите на онези бикове, които Питагор, възхитен от откритието на своята теорема, принесе в жертва на безсмъртните богове.
И въпреки че днес теоремата на Питагор се намира в различни конкретни проблеми и рисунки: както в египетския триъгълник в папируса от времето на фараона Аменемхет I (ок. 2000 г. пр.н.е.), така и във вавилонския клинописплочи от епохата на цар Хамурапи (XVIII век пр. н. е.) и в древния китайски трактат "Джоу-би суан дзин" ("Математически трактат за гномона"), времето на създаване на което не е точно известно, но където се посочва, че през XII век. пр.н.е д. китайците познават свойствата на египетския триъгълник и до VI век. пр.н.е д. - и общата форма на теоремата, и в древноиндийския геометрико-теологичен трактат от 7 - 5 век. пр.н.е д. "Sulva Sutra" ("Правила на въжето") - въпреки всичко това името на Питагор е толкова здраво слято с Питагоровата теорема, че сега е просто невъзможно да си представим, че тази фраза ще се разпадне. Същото се отнася и за легендата за клането на бикове от Питагор. И едва ли е необходимо да се правят дисекции на красиви древни легенди с историко-математически скалпел.
Днес е общоприето, че Питагор е дал първото доказателство на теоремата, носеща неговото име. Уви, не е оцеляла и следа от това доказателство. Следователно не ни остава нищо друго освен да разгледаме някои от класическите доказателства на Питагоровата теорема, известни от древните трактати. Също така е полезно да се направи това, защото съвременните училищни учебници дават алгебрично доказателство на теоремата. В същото време първичната геометрична аура на теоремата изчезва безследно, онази нишка на Ариадна, която е довела древните мъдреци до истината, се губи и този път почти винаги се оказва най-краткият и винаги красив. Така,
Питагоровата теорема.Квадратът, построен върху хипотенузата на правоъгълен триъгълник, е равен на сбора от квадратите, построени върху неговите катети.
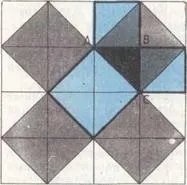
Най-простото доказателство на теоремата се получава в най-простия случай на равнобедрен правоъгълен триъгълник. Вероятно теоремата започва с него. Наистина, достатъчно е просто да погледнете мозайката от равнобедрени правоъгълни триъгълници (фиг. 56),за проверка на валидността на теоремата. Например за !ABC: квадратът, построен върху хипотенузатаAC, съдържа 4 начални триъгълника, а квадратите, построени върху катетите, съдържат два. Теоремата е доказана.
В IX книга на "Математика" има чертеж (фиг. 57,a), доказващ Питагоровата теорема. Ключът към това доказателство не е трудно да се намери. Наистина, в древен китайски чертеж четири равни правоъгълни триъгълника с катетиa,bи хипотенузаcса подредени така, че външният им контур образува квадрат със страна , а вътрешният образува квадрат със странаc, изградена върху хипотенузата (фиг. 57,b). Ако се изреже квадрат със странаcи останалите 4 защриховани триъгълника се поставят в два правоъгълника (фиг. 57,c), тогава е ясно, че получената празнина, от една страна, е равна на , а от друга, т.е. Теоремата е доказана.
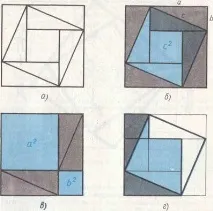
Имайте предвид, че при такова доказателство не се използват конструкциите вътре в квадрата върху хипотенузата, които виждаме в древния китайски чертеж (фиг. 57,a). Очевидно древните китайски математици са имали друго доказателство. А именно, ако в квадрат със странаcдва защриховани триъгълника (фиг. 57,b) се отрежат и се прикрепят с хипотенузи към две други хипотенузи (фиг. 57,d), тогава е лесно да се установи, че получената фигура, която понякога се нарича "столът на булката", се състои от два квадрата със страниaиb, i .е.
Фигура 58 възпроизвежда рисунка от трактата „Джоу-би. ". Тук се разглежда Питагоровата теорема за египетския триъгълник с катети 3, 4 и хипотенуза 5 единици. Квадратът върху хипотенузата съдържа 25 клетки, а квадратът, вписан в него върху по-големия катет, съдържа 16. Ясно е, че останалата част съдържа 9 клетки. Това ще бъдеквадрат на по-малкия крак.
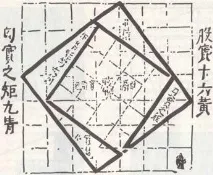
Ориз. 58. „Питагоровата теорема” в древнокитайския трактат „Джоу-би суан дзин”.
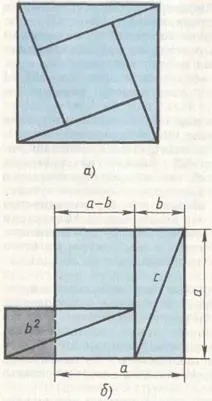
Древноиндийско доказателство. Математиците от Древна Индия са забелязали, че за да се докаже Питагоровата теорема, е достатъчно да се използва вътрешността на древен китайски чертеж. В трактата Сидханта Широмани (Корона на знанието), написан върху палмови листа, от най-великия индийски математик от 12 век. Bhaskara съдържа рисунка (фиг. 59,a) с думата „вижте!“, характерна за индийските свидетелства. Както можете да видите, правоъгълните триъгълници са положени тук с хипотенузата им навън и квадратът е изместен в "стола на булката" (фиг. 59,b). Имайте предвид, че специални случаи на Питагоровата теорема (например изграждането на квадрат, чиято площ е два пъти по-голяма от площта на дадения квадрат - фиг. 60) се намират в древния индийски трактат "Sulva Sutra" (7-ми - 5-ти век пр.н.е.).
Доказателството на Евклид е дадено в изречение 47 от книга I от Началата. Върху хипотенузата и катетите на правоъгълния триъгълникABC(фиг. 61) са построени съответните квадрати и е доказано, че правоъгълникътBJLDе равен на квадратаABFH, а правоъгълникътJCELе равен на квадратаACKG. Тогава сборът от квадратите на катетите ще бъде равен на квадрата на хипотенузата. Наистина триъгълницитеABDиBFC, защриховани на фигурата, са равни по две страни и ъгъла между тях: , и . Но тъй като триъгълникътABDи правоъгълникътBJLDимат обща основаBDи обща височинаLD. По същия начин (BFе общата основа,ABе общата височина). Следователно, като се има предвид, че имаме . По същия начин, използвайки равенството на триъгълнициBCKиACE, доказваме, че .
И така, това е, което искахме да докажем.
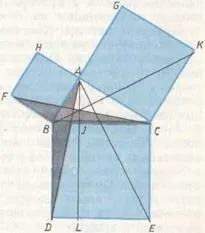
ДоказателствоЕвклид, в сравнение с древния Китай или древна Индия, изглежда прекалено сложен. Поради тази причина той често е бил наричан "надукан" и "пресилен". Но такова мнение е повърхностно. Питагоровата теорема на Евклид е последната брънка във веригата от изречения в книга I от Началата. За да изгради тази верига логически безупречно, така че всяка стъпка от доказателството да се основава на предварително доказани твърдения, Евклид се нуждаеше точно от пътя, който беше избрал. Читателят може самостоятелно да провери това, като прочете книга I от „Началата“ и изгради верига от разсъждения, подобна на (2.3.1).
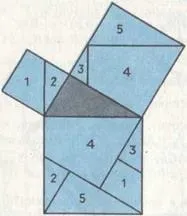
Методът на еднакво съставените фигури е бил много популярен в древността. Вероятно по това време е изобретен пъзелът, известен днес като "Питагор". Лесно се вижда, че седемте части на пъзела се основават на равнобедрен правоъгълен триъгълник и квадрати, изградени върху краката му, или, с други думи, фигури, съставени от 16 еднакви равнобедрен правоъгълен триъгълник и следователно се вписват в квадрат.
Това е само малка част от богатството, скрито в перлата на древната математика – Питагоровата теорема. Неслучайно на корицата на последното издание на Математическия енциклопедичен речник (М.: SE, 1988) със златни линии е възпроизведена рисунка от древнокитайското доказателство на Питагоровата теорема като символ на математиката.
Но защо всички древни доказателства на Питагоровата теорема са геометрични? Защо древните гърци са се страхували толкова много от алгебрата и всъщност са я свели до геометрия? Това са много важни въпроси, които определят цялото по-нататъшно развитие на древната математика след Питагор, чието име егеометрична алгебра.
Не намерихте това, което търсихте? Използвайте търсачката: