Полуправилни политопи - Студиопедия

Лаборатория #9(5 MT)

• Построяване на полуправилни многостени по системата Mathematica;
• Развийте пространственото въображение чрез този пакет.

Полуправилен полиедъре изпъкнал многостен, чиито лица са правилни многоъгълници, вероятно с различен брой страни, и един и същ брой лица се събират във всеки връх. Полуправилните полиедри включват правилни n-въглищни призми, всички ръбове на които са равни. Полуправилните полиедри включват и така наречените антипризми с равни ръбове.

В допълнение към тези две безкрайни серии от полуправилни многостени, има още четиринадесет полуправилни многостени, тринадесет от които са открити и описани за първи път от Архимед - това са телата на Архимед. Най-простите от тях се получават от правилни многостени чрез операцията на отрязване, която се състои в отрязване на ъглите на многостена с равнини.

Ако срежем ъглите на тетраедъра с равнини, всяка от които отрязва третата част от ръбовете му, излизащи от един връх, ще получимпресечен тетраедър- фиг.1, имащ осем лица. Командата за отрязване е Truncate.

фиг. 1. Пресечен тетраедър

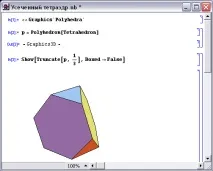
Ако отрежем върховете на останалите четири правилни многоъгълника по същия начин, получаваме съответно пресечен куб, пресечен октаедър, пресечен икосаедър, пресечен додекаедър.

Фигура 2 показвапресечен куб- в този случай ъглите на оригиналния куб са отрязани от равнини, всяка от които отрязва една трета от ръбовете му, излизащи от един връх.

фиг. 2. Срязан куб

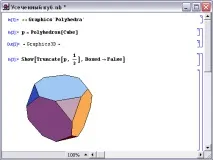
Фигура 3 показвапресечен октаедър(фактор на отрязване - 0.3).

фиг.3. Пресечен октаедър

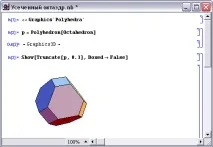
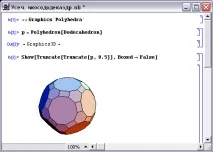
Фигура 4 показвапресечен икосаедър(коефициент на отрязване - 0.3), а фигура 5 -пресечен додекаедър(коефициент на отрязване - 0.3).

фиг. 4. Пресечен икосаедър

фиг. 5. Пресечен додекаедър

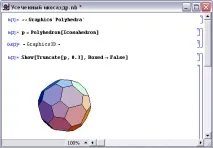
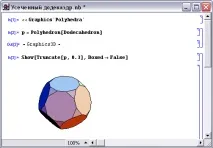
За да получим още един полуправилен многостен, начертаваме режещи равнини в куба през средните точки на ръбовете, излизащи от един връх. В резултат на това получаваме полуправилен многостен, който се наричакубооктаедър- фиг. 6.

фиг. 6. Кубоктаедър

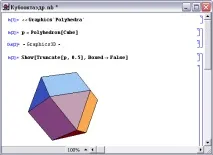
По същия начин, ако секущи равнини в додекаедър се начертаят през средните точки на ръбове, излизащи от един връх, тогава получаваме многостен, който се наричаикозидодекаедър- фиг.7. Той има двадесет лица - правилни триъгълници и дванадесет лица - правилни петоъгълници, тоест всички лица на икосаедъра и додекаедъра.

фиг. 7. Икозидодекаедър

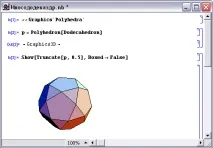
Последните два полиедра могат отново да бъдат съкратени. Получавамепресечен кубоктаедър- фиг.8 ипресечен икозидодекаедър- фиг.9.

фиг. 8. Пресечен кубоктаедър

фиг. 9. Пресечен икозидодекаедър

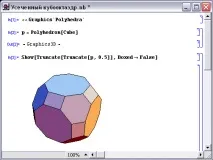
Разгледахме 9 от 13-те полуправилни полиедра, описани от Архимед. Четирите останали разновидности на полиедри са полиедри от по-сложен тип. Тези полиедри са:ромбокубооктаедър, ромбикозидодекаедър, изпъкнал (изпъкнал) куб, изпъкнал (изпъкнал) додекаедър.

Не намерихте това, което търсихте? Използвайте търсачката:

Деактивирайте adBlock! и обновете страницата (F5)наистина е необходимо

---