Прави и равнини

Начини за определяне на равнина

Една равнина в пространството е уникално дефинирана:

три точки, които не лежат на права и точка, която не лежи

на една права линия на тази права линия

две пресичащи се прави две успоредни прави

Прави линии в пространството

Знак за успоредни прави:

Две прави, успоредни на трета права, са успоредни една на друга:

Права и равнина в пространството

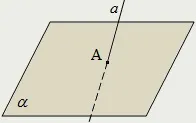
Ако две точки от една права принадлежат на равнина, то цялата права принадлежи на тази равнина:

Точка A се нарича пресечната точка на правата и равнината или следата на правата a върху равнината α.

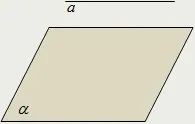
Права и равнина се наричат успоредни, ако нямат общи точки:

Равнина и права, която не лежи върху нея, се пресичат (в една точка) или не се пресичат (успоредно).

Знак за успоредност на права и равнина:

Права, която не лежи в равнина, е успоредна на тази равнина тогава и само ако е успоредна на някаква права в тази равнина:

Знак за успоредни прави:

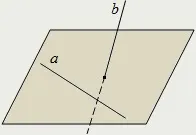
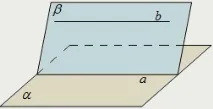
Ако правата b е успоредна на равнината α, а равнината β минава през b и пресича равнината α по правата a, то правите a и b са успоредни:

Знак за успоредни прави:

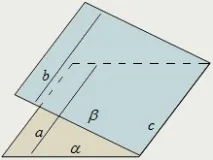
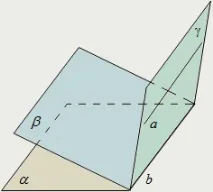
Ако правата е успоредна на всяка от двете пресичащи се равнини, тогава тя е успоредна и на пресечната линия на тези равнини:

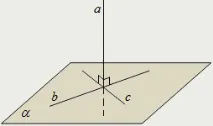
Права, пресичаща равнина, се нарича перпендикулярна на тази равнина, ако е перпендикулярна на всяка права, която лежи в дадената равнина и минава през пресечната точка на тази права и равнината.

През всяка точка в пространствотоначертайте линия, перпендикулярна на дадена равнина, и освен това само една.

Знак за перпендикулярност на права и равнина:

Ако една права е перпендикулярна на две пресичащи се прави, лежащи в равнина, то тя е перпендикулярна на дадената равнина:

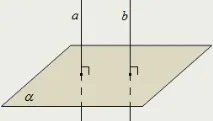
Равнина, перпендикулярна на една от двете успоредни прави, също е перпендикулярна на другата права:

Правите, перпендикулярни на една и съща равнина, са успоредни:

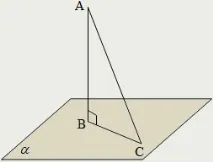
Перпендикуляр, прекаран от дадена точка към дадена равнина, е отсечка, която свързва тази точка с точка в равнината (основата на перпендикуляра) и лежи на права линия, която е перпендикулярна на равнината. Дължината на перпендикуляр, прекаран от дадена точка към дадена равнина, се счита за разстоянието между тази точка и равнината.

Наклонена, прекарана от дадена точка към равнина, е всеки сегмент, който свързва тази точка с точка в равнината (основата на перпендикуляра) и не е перпендикуляр, прекаран към тази равнина.

Отсечката, свързваща основите на перпендикуляра и наклонената, начертана към равнината от една точка, се нарича проекция (ортогонална проекция) на тази наклонена върху равнината.

AB е перпендикуляр, прекаран от точка A към равнината α;

AC - наклонена, изтеглена от точка A към равнината α;

B - основата на перпендикуляра AB;

C - основата на наклонената АС;

BC е проекцията на наклонената AS върху равнината α .

Перпендикулярни и наклонени свойства:

перпендикуляр, прекаран от точка към равнина, е по-къс от всеки наклонен, прекаран от същата точка към същата равнина;
равни наклонени, изтеглени от дадена точка към равнина, имат равни проекции; и обратно: равни проекции съответстват на равнинаклонен;
от две наклонени прави, прекарани от дадена точка към една и съща равнина, по-голямата е тази, чиято проекция е по-голяма.

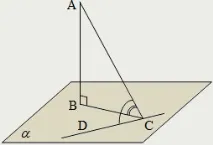
Ъгълът между наклонената и равнината е стойността на ъгъла между наклонената и нейната ортогонална проекция върху тази равнина:

Ъгълът между наклонената и нейната ортогонална проекция върху равнина е по-малък от ъгъла между тази наклонена и всяка друга права линия, минаваща в тази равнина през основата на наклонената:

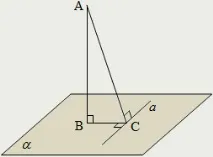
Теорема за три перпендикуляра:

Ако права линия, начертана в равнина през основата на наклонена, е перпендикулярна на нейната проекция, то тя е перпендикулярна и на самата наклонена. И обратно: ако права, прекарана в равнина през основата на наклонена, е перпендикулярна на наклонената, то тя е перпендикулярна и на проекцията на тази наклонена:

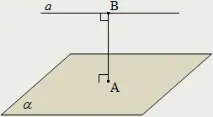
Разстоянието от права линия до успоредна на нея равнина е разстоянието от всяка точка на тази права линия до равнина:

AB е разстоянието от правата a до равнината α.

Отсечката AB е общият перпендикуляр на правата a и равнината α.

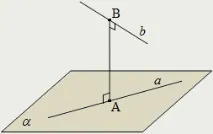
Общият перпендикуляр на две пресичащи се прави ( a и b ) е отсечка ( AB ) с краища на тези прави, която е перпендикуляр на всяка от тях.

Две пресичащи се прави винаги имат общ перпендикуляр и освен това само един.

Дължината на общия перпендикуляр на две пресичащи се прави се счита за разстоянието между тях:

AB е разстоянието между пресичане на a и b.