ПРИЛОЖЕНИЕ НА ТЕОРИЯТА НА ИНЖЕНЕРНИЯ ДИСКРИМИНАНТ В ПРИЛОЖНИТЕ ИЗЧИСЛЕНИЯ

ПРИЛОЖЕНИЕ НА ТЕОРИЯТА НА ИНЖЕНЕРСТВОТОДИСКРИМИНАНТ В ПРИЛОЖНИТЕ ИЗЧИСЛЕНИЯ

Попова Людмила Силвестровна

Доктор, доцент, VyatGU, Киров

Олга Владимировна Синицина

Доктор, доцент, VyatGU, Киров

Основната задача на разработването на сложни плоски и пространствени контури е да се създаде техният оптимален математически модел в рамките на съществуващите системи за компютърно проектиране. Необходими са системни изследвания в тази област за модернизиране на автоматизираните изчислителни системи и контрол на работата на различни обекти и процеси.

150%"> За постигане на оптимални резултати на етапа на проектиране на самите обекти е възприета следната последователност от конструктивни действия:

1. въз основа на предоставената графична информация и уводни спецификации се проектира математически модел на разработвания обект;

2. Според емпиричните данни, получени в резултат на апробацията на обекта, се финализират неговите необходими свойства.

При проектирането на сложни повърхности на рационализирани технически конструкции като кораби и самолети, на първо място, е необходимо да се вземе предвид набор от специални изисквания. Специалните условия за проектиране на контури на такива повърхности с определена степен на гладкост определят създаването на нови графични и аналитични алгоритми за тяхното моделиране.

В предишни работи [2, p. 322] се предлага да се опишат сложни геометрични повърхности в матрична нотация. Аналитичното описание на повърхността в матрична форма осигурява достатъчно висока степен на формализиране на решението на проблемите при свързване на части от повърхности с дадена степен на гладкост в равнинипроизволна позиция.

150%;tab-stops:36.0pt"> За разработването на сложни повърхности имплицитно дефинирани криви и повърхности от втори ред са намерили голямо практическо приложение.

150%;tab-stops:36.0pt"> Да разгледаме метод, базиран на използването на сегменти от конични сечения, които отговарят на условията за конюгиране и допиране в няколко точки. Както знаете, криви от втори ред могат да бъдат получени чрез разделяне на конична повърхност на въртене с различни равнини. В зависимост от местоположението на режещата равнина и оригиналната конична повърхност, получаваме:

• кръг, ако режещата равнина е перпендикулярна на оста на въртене на конуса;
• елипса, ако сечащата равнина пресича всички генератори на конуса на конуса;
• парабола, ако сечащата равнина е успоредна на една от образуващите на конуса;
• хипербола, ако секателната равнина е успоредна на две образуващи на конуса.

За да се получи желаното уравнение, се използват сегменти от конични сечения, които отговарят на условията за конюгиране и допиране в няколко дадени точки.

Общите конични сечения се описват с уравнение от втори ред в неявна форма [3, p. 18]:

(1)

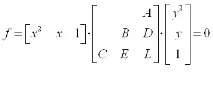
нормален">ABCDEL. За да се намерят тези коефициенти, е необходимо да се наложат пет независими условия и да се решат съответните уравнения за съотношенията на тези коефициенти към едно от тях. Тази операция е доста трудоемка.

150%"> За да избегнете решаването на система от уравнения, можете да използватекласическа техника, която показва предимствата на уравненията, дадени в неявна форма [4, p. 81].

150%"> Нека две конични сечения (фиг. 1) са дадени от уравнениятаf1 (x,y)=0 иf2 (x,y)=0, или накраткоf1=0,f2 =0.

150%"> Тези криви се пресичат в четири точки, през които могат да бъдат начертани множество конични сечения, включително изродените конични сечения, които са резултат от пресичането на конус с равнина, минаваща през неговия връх.

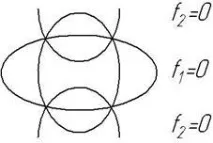
Уравнението на този лъч има формата:

(1–λ)f+λf=0,

където λ е инженерен дискриминант, който може да се използва за контролиране на формата на кривите на даден лъч.

150%"> Уравнението е валидно за точките, принадлежащи наf1=0 иf2=0. Това уравнение удовлетворява още едно конично сечение, преминаващо през пресечните точки на кривитеf1=0 иf2=0 за всякакви стойности на λ.

150%"> В инженерна версия крива от втори ред може да бъде дефинирана от триъгълникABCи дискриминантλ. Нека разгледаме тази разпоредба с помощта на пример (фиг. 2). Нека зададем криваlот втори ред чрез точкиA, CиF, както и тангентиl1иl2(ABиBC) в точкиAиnormal">C.

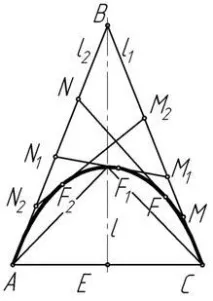
150%"> Нека изберем точкаFвътре в триъгълникаABC, тогава коничното сечение образува непрекъсната крива между точкитеAиCвътре в триъгълника. gt;F е между тази парабола и праватаnormal">AC, тогава се получава елипса. Ако товаточката е извън параболата, тогава се получава хипербола.

150%"> Задавайки началната позиция на точкатаF, определяме коефициента λ, който се намира от връзката:

където λ е техническият дискриминант на дъгатаACот крива от втори ред, определена от съседния триъгълникABCи точкатаF.

150%"> Избирайки различни позиции на точкатаF, можете да зададете формата на дъгата на проектираната крива от втори ред - елипса, парабола, хипербола.

150%;tab-stops:54.0pt"> Нека разгледаме алгоритъма за проектиране на криваl, дадена от координатите на необходимия брой точки.

150%;tab-stops:54.0pt"> Известно е, че тази криваlминава през точкитеnormal">A,normal">Cиnormal">F. ПравитеABиBC(l1 иl2) са допирателните към криватаl, начертани в точкитеnormal">AиC, и линиитеMiNiдопирателни към криватаlв точкиFi.

150%"> ТочкаF, удовлетворява системата от три отношения:

(2)

Нека построим във всяка точкаFiот криватаlдопирателна праваMiNi. Нека означим сегментиFNиnormal">FMвърху него, така чеnormal">NMK=µ. Ако през получените точкиnormal">Mиnormal">Nпрекараме допирателни към криватаl, то получаваме триъгълникACB, в който се запазват равенства (2).

Представеният алгоритъм дава възможност да се построят точки от криватаnormal">l, разположени както вътре в триъгълникаACB,, така и извън него.

150%"> Една от задачите на съвременната приложна геометрия е да реши проблема с аналитичното и графично дефиниране на затворени контурисложни форми. При проектирането на фюзелаж на самолет конфигурацията на всяка секция е съставена от криви от втори ред, които имат общи допирателни в кръстовищата и един и същ радиус на кривина. Решението на задачата се свежда до изграждането на криви с помощта на фигурата от постоянни елементи, състояща се от точкаFи съседен триъгълникABC[1, с. 45, 46].

150%;tab-stops:36.0pt"> Разглежданият алгоритъм позволява да се получат уравненията на кривите, апроксимиращи контурите на теоретичните напречни сечения (например контурите на рамите на фюзелажа на самолет) с дадена точност.

150%;tab-stops:36.0pt"> Разработеният от нас математически апарат за геометрично моделиране на сложни контури може успешно да се използва и за управление на изчисленията на траекторията на полета на геометрични обекти на големи разстояния.

150%;tab-stops:36.0pt"> Помислете например за траекторията на полета на самолет, когато лети от една планета на друга. Според геометрията на Лобачевски, като се вземе предвид кривината на пространството, траекторията на полета на въпросния обект е една от кривите на повърхността на конуса - елипса, хипербола или парабола.

150%;tab-stops:36.0pt"> Ако самолет трябва да лети около интересна планета и да се върне, траекторията му на полета ще бъде елипсовидна крива. Когато обект е планирано да кацне на планета, самолетът трябва да лети в парабола.

150%;tab-stops:36.0pt"> На Фиг. 3 условната траектория на полета на въздухоплавателното средство се разглежда по протежение на вариантната крива от втори редAB.

табулатори: 36.0pt 439.45pt">

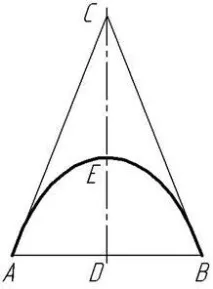
150%"> За изчисляване на полета на геометричен обект от точкаAдо точкаBпопарабола, хипербола или елипса, ние използваме отношенията на инженерния дискриминантλ.

150%"> За да определим графичния дискриминантλ, ще образуваме триъгълникABC. Първо, свържете точкитеAиBс права линия и след това начертайте допирателни линии и медианаC D в крайните точки на дъгата. 4>AB.

150%"> Съотношението на сегментитеDEкъмCDсе нарича графичен или инженерен дискриминантλ.

150%"> Варианти на стойностите на съотношениятаλ=DE/CDна инженерния дискриминант и ни дават решения на проблема.

150%"> Разглежданата точкаEсе намира в триъгълникаABCи принадлежи на коничното сечение, образуващо непрекъсната крива между точкитеAиBвътре в триъгълника.

150%"> Ако точкатаEразполовява правата, свързваща средните точки на отсечките AC иCB, тогава коничното сечение, минаващо през тази точка, е парабола.

150%"> Ако точкатаEе между тази парабола и линиятаnormal">CD, тогава получената крива ще бъде елипса.

150%"> Ако тазиEточка е извън параболата, тогава коничната крива, минаваща през тази точка, ще бъде хипербола.

150%"> По този начин изборът на точкаEе пряко свързан със стойностите на инженерния дискриминантλ,, който е от отношението наDEкъмCD.

150%"> От аналитичната геометрия е известно, че характерът на кривата от втори ред на дъгатаAB

150%"> Например, ако стойността на дискриминанта е в рамките на0 Тази опция за симулация на траекторията на полета позволява не само изчисляване на траекторията на самолета, но и намаляване на количеството скъпо гориво, намаляване на устойчивостта на външни фактори като температура, гравитация и т.н.

150%;tab-stops:36.0pt"> По този начин оптималният математически модел на проектирания байпас на кривата на полета ви позволява да превключите към автоматична система за свързване на параметрите, които го определят.

150%;tab-stops:36.0pt"> Въз основа на графични конструкции е необходимо да се разработят всички видове алгоритми за математическо решаване на поставените задачи. Избраният подход в процедурата за формализиране на горния проблем позволява използването на по-малко енергоемки програми, което прави проектирането по-икономично.

1. Левицки В. С. Аналитични методи в инженерната графика [Текст]: учебник. ръководство по курса "Инженерна графика" за студенти от FPKP / V. S. Levitsky. - М.: Издателство на МАИ, 1978. - С. 43-47.

3. Изграждане на плосък байпас от втори ред с помощта на инженерен дискриминант [Текст] / L. S. Popova, O. V. Sinitsyna // Наука - производство - технология - екология: All-Russian. годишно наук.-техн. конф. сб. материали в 7 тома Т. 4. ФАМ, ФСА / Вятски държавен университет. - Киров, 2008. - С. 321-323.

4. Попова Л. С. Някои въпроси на проектирането на повърхности на технически конструкции [Текст]: дис. … канд. техн. науки: 05.01.01: защитена 18.06.1981: утв. 30.09.1981 г. / Л. С. Попова.- М., 1978. - Библиография: с. 16-26.

-1.0cm;line-height:150%;mso-list:l1 level1 lfo2;tab-stops:list 1.0cm 36.0pt">

---