Принудителни вибрации
Трептенията, които възникват под въздействието на външна периодична сила, се наричат принудени.
Външната сила извършва положителна работа и осигурява приток на енергия към трептящата система. Не позволява трептенията да избледняват, въпреки действието на силите на триене.
Периодичната външна сила може да варира във времето според различни закони. От особен интерес е случаят, когато външна сила, която се променя по хармоничен закон с честота ω, действа върху колебателна система, способна да извършва собствени трептения с определена честота ω0.
Ако свободните трептения възникват при честота ω0, която се определя от параметрите на системата, тогавапостоянните принудителни трептения винаги възникват при честота ω на външната сила.
След началото на въздействието на външна сила върху трептящата система е необходимо известно време Δt за установяване на принудени трептения. Времето на установяване е равно по порядък на времето на затихване τ на свободните трептения в трептящата система.
В началния момент в колебателната система се възбуждат и двата процеса - принудени трептения с честота ω и свободни трептения със собствена честота ω0. Но свободните вибрации се гасят поради неизбежното наличие на сили на триене. Следователно след известно време в трептящата система остават само стационарни трептения с честотата ω на външната движеща сила.
Да разгледаме като пример принудени вибрации на тяло върху пружина (фиг. 2.5.1). Към свободния край на пружината се прилага външна сила. Той принуждава свободния (вляво на фиг. 1.2.11) край на пружината да се движи по закона
където ym е амплитудата на трептене, ω е кръговата честота.
Такъв закон на изместване може да се осигури с помощта на свързващ прътмеханизъм, който не е показан на фиг. 1.2.11.
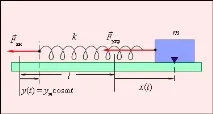
Принудени вибрации на товар върху пружина. Свободният край на пружината се движи по закона y = ymcos ωt. l е дължината на недеформираната пружина, k е твърдостта на пружината.
Ако левият край на пружината е изместен на разстояние y, а десният край на разстояние x от първоначалното им положение, когато пружината е била недеформирана, тогава удължението на пружината Δl е:
Δl = x – y = x – ym cos ωt.
Вторият закон на Нютон за тяло с маса m:
ma = –k(x – y) = –kx + kym cos ωt.
В това уравнение силата, действаща върху тялото, е представена като два члена. Първият член от дясната страна е еластичната сила, стремяща се да върне тялото в равновесно положение (x = 0). Вторият термин е външното периодично въздействие върху тялото. Този термин се наричадвижеща сила.
Уравнението, изразяващо втория закон на Нютон за тяло върху пружина при наличие на външно периодично действие, може да получи строга математическа форма, ако вземем предвид връзката между ускорението на тялото и неговата координата: Тогавауравнението на принудените трептенияще бъде записано във формата
където е естествената кръгова честота на свободните трептения, ω е цикличната честота на движещата сила. В случай на принудителни вибрации на товара върху пружината (фиг. 2.5.1), стойността на A се определя от израза:
Уравнението не отчита действието на силите на триене. За разлика от уравнението на свободните трептения, уравнението на принудителните трептениясъдържа две честоти - честотата ω0 на свободните трептения и честотата ω на движещата сила.
Равномерните принудителни вибрации на товара върху пружината възникват при честотата на външното въздействие според закона
Амплитудата на принудените трептения xm и началната фаза θ зависят от съотношението на честотите ω0 и ω и от амплитудата ym на външната сила.
Намного ниски честоти, когато ω
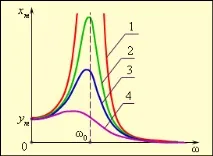
Резонансни криви при различни нива на затихване: 1 – колебателна система без триене; при резонанс амплитудата xm на принудените трептения нараства неограничено; 2, 3, 4 - реални резонансни криви за осцилаторни системи с различни качествени фактори: Q2> Q3> Q4. При ниски честоти (ω > ω0) xm→ 0.
Принудените трептения санезатихващитрептения. Неизбежните загуби на енергия поради триене се компенсират чрез доставка на енергия от външен източник на периодично действаща сила. Има системи, в които незатихващите трептения възникват не поради периодично външно влияние, а в резултат на способността на такива системи да регулират потока на енергия от постоянен източник. Такива системи се наричатавтоколебателни, а процесът на незатихващи трептения в такива системи се наричаавтоколебания.
В една автоколебателна система могат да се разграничат три характерни елемента - трептителна система, източник на енергия и устройство за обратна връзка между трептящата система и източника. Като осцилаторна система може да се използва всяка механична система, способна да извършва собствени затихващи трептения (например махало на стенен часовник). Източникът на енергия може да бъде енергията на деформация на пружината или потенциалната енергия на товара в гравитационното поле. Устройството за обратна връзка е механизъм, чрез който автоколебателната система регулира потока на енергия от източника. На фиг. 1.2.13 показва диаграма на взаимодействието на различни елементи на самоколебателна система.
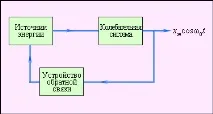
Функционална схема на автоколебателна система.
Пример за механична самоосцилираща система е часовников механизъм санкеренпът (фиг. 1.2.14). Работно колело с наклонени зъби е здраво закрепено към зъбен барабан, през който се хвърля верига с тежест. В горния край на махалото е фиксирана котва (котва) с две пластини от твърд материал, огънати по дъга от окръжност, центрирана върху оста на махалото. В ръчния часовник тежестта е заменена от пружина, а махалото е заменено от балансьор - ръчно колело, закрепено към спирална пружина. Балансьорът извършва усукващи вибрации около оста си. Осцилаторната система в часовника е махало или балансьор. Източникът на енергия е вдигната тежест или навита пружина. Устройството за обратна връзка е анкер, който позволява на ходовото колело да завърти един зъб за един половин цикъл. Обратната връзка се осигурява от взаимодействието на котвата с движещото се колело. При всяко колебание на махалото зъбът на ходовото колело избутва вилицата на котвата по посока на движението на махалото, като му предава определена част от енергията, която компенсира загубите на енергия от триене. Така потенциалната енергия на тежестта (или усуканата пружина) постепенно, на отделни порции, се предава на махалото.
Механичните автоколебателни системи са широко разпространени в живота около нас и в техниката. Самоколебанията се извършват от парни машини, двигатели с вътрешно горене, електрически звънци, струни на лъкови музикални инструменти, въздушни колони в тръбите на духови инструменти, гласни струни при говор или пеене и др.
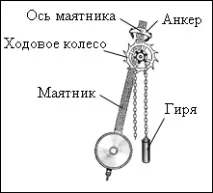
Часовников механизъм с махало.
ЗАДАЧА: Изведете формула за цикличната честота на свободните трептения на куб върху пружина, лежащ върху хоризонтална абсолютно гладка повърхност.
УКАЗАНИЯ: Запишете формулата за втория закон на Нютон. Заместете в него всички реални действащи силина куб. Проектирайте полученото векторно уравнение върху вертикалната и хоризонталната ос. След като извършите идентични трансформации, ще получите уравнение, подобно на диференциалното уравнение на свободните вибрации. Приравнете константата, която е множител пред А, на квадрата на цикличната честота, от което получавате .
МЕТОД И РЕД НА ИЗМЕРВАНИЯ
Внимателно разгледайте снимките, намерете всички контроли и други основни елементи. Скицирайте полето на движение на тялото с контролите на съответните параметри (посочете какво регулират).
Изберете „Махало“. Използвайте плъзгачите, за да зададете максималната дължина на резбата L и стойностите на коефициента на затихване и началния ъгъл, посочени в таблицата. 1 за вашия отбор.
Като щракнете с мишката върху бутона "СТАРТ", проследете движението на точката върху графиките на ъгъл и скорост и поведението на махалото. Практикувайте спиране на движението с бутона "СТОП" (например при максимално изместване) и започване по-нататък с бутона "СТАРТ". Изберете броя на пълните трептения N= 3 - 5 и измерете тяхната продължителност t (като разлика t2-t1 от таблицата на екрана).
Помолете вашия учител за разрешение да направите измервания.
Започнете да измервате продължителността t за N (3-5) пълни трептения, като започнете с максималната дължина (150 cm) на нишката на махалото и я намалявате с 10 cm всеки път (до минимална дължина от 80 cm). Запишете дължината на нишката L и резултатите от измерванията на продължителността t в таблица 2, чиято проба е дадена по-долу.
Изберете тегло на пружината. Задайте масата на товара, стойността на коефициента на затихване и първоначалното изместване, посочени в таблицата. 1 за вашия отбор. Извършете измервания, подобни на експеримент 1, като намалявате коефициента на коравина k всеки път с 1 N/m.
Таблица 1. Стойностикоефициент на затихване (вискозно триене), начален ъгъл на отклонение (за първия експеримент) и начално отклонение (за втория).