проекционен чертеж
Дескриптивната геометрияизучава как да се конструират изображения на пространствени фигури в равнина и да се решават пространствени проблеми в чертеж.
Проекционният чертежразглежда практическите въпроси на конструирането на чертежи и решава проблеми по начините, разглеждани в описателната геометрия, първо върху чертежите на геометрични тела, а след това върху чертежите на модели и технически детайли.
Методи за получаване на графични изображения
Формата на всеки обект може да се разглежда като комбинация от отделни прости геометрични тела. А за да изобразите геометрични тела, трябва да можете да изобразите отделните им елементи: върхове (точки), ръбове (прави линии), лица (равнини).
В основата на изграждането на изображения е методът на проекцията. За да получите изображение на обект означава да го проектирате върху равнината на чертежа, т.е. проектират отделните му елементи. Тъй като най-простият елемент на всяка фигура е точка, изучаването на проекцията започва с проекцията на точка.
За да се получи изображение на точка А в равнината Р (фиг. 4.1), през точка А се изчертава изпъкнал лъч Аа. Пресечната точка на проектиращия лъч с равнината P ще бъде изображението на точка A в равнината P (точка a), т.е. нейната проекция върху равнината P.
Този процес на получаване на изображение (проекция) се нарича проекция. Равнината P е равнината на проекцията. Върху него се получава изображение (проекция) на обект, в случая точка.
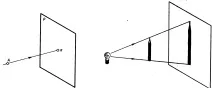
Принципът на проекцията е лесен за разбиране чрез примера за получаване на сянка на обект върху стена или лист хартия. На фиг. 4.1 показва сянката на молив, осветен от лампа, а на фиг. 4.2 - сянката на молив, осветена от слънчева светлина. Ако си представим светлинните лъчи като прави линии, тоест като прожектиращи лъчи, а сянката като проекция(изображение) на обект върху равнина, лесно е да си представим механизма на проекцията.
В зависимост от взаимното разположение на проектиращите лъчи проекцията се дели на централна и успоредна.
Централна и странична проекция
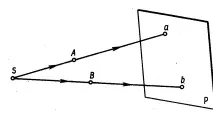
Централна проекция- получаване на проекции с помощта на проектиращи лъчи, преминаващи през точката S, която се нарича център на проекцията (фиг. 4.3). Ако разглеждаме лампата като точков източник на осветление, тогава проектиращите лъчи излизат от една точка, следователно централната проекция на молива се получава върху равнината P (фиг. 4.1).
Пример за централна проекция е проекцията на филмови кадри или диапозитиви върху екран, където рамката е обект на проекция, изображението на екрана е проекцията на рамката, а фокусът на лещата е центърът на проекцията.
Изображенията, получени чрез метода на централната проекция, са подобни на изображенията върху ретината на нашето око. Те са ясни, разбираеми за нас, тъй като ни показват обектите на заобикалящата ни действителност така, както сме свикнали да ги виждаме. Но изкривяването на размера на обектите и сложността на изграждане на изображения с централна проекция не позволяват да се използва за правене на чертежи.
Централните проекции се използват широко само там, където е необходима яснота на изображенията, например в архитектурни и строителни чертежи при изобразяване на перспективи на сгради, улици, площади и др.
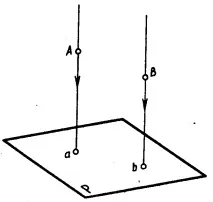
Паралелна проекция. Ако центърът на проекцията - точка S се отдалечи до безкрайност, тогава проектиращите лъчи ще станат успоредни един на друг. На фиг. 4.4 показва получаването на успоредни проекции на точки A и B върху равнината P.
В зависимост от посоката на проектиращите лъчи спрямо проекционната равнинапаралелните проекции са разделени накоси и правоъгълни.
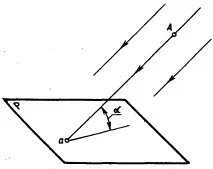
Принаклонена проекцияъгълът на наклона на проектиращите лъчи към равнината на проекцията не е равен на 90 ° (фиг. 4.5).
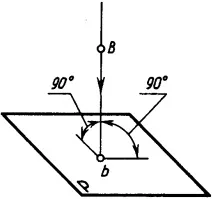
При правоъгълна проекция проектиращите лъчи са перпендикулярни на проекционната равнина (фиг. 4.6).
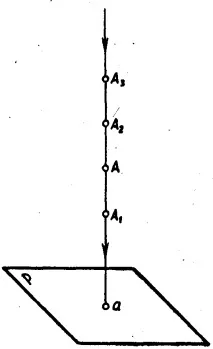
Методите за проектиране, разгледани по-горе, не установяват съответствие едно към едно между обект (точка А) и неговото изображение (проекция). При дадена посока на проектиращите лъчи върху проекционната равнина винаги се получава само една проекция на точката, но е невъзможно да се прецени позицията на точката в пространството по нейната една проекция, тъй като на един и същ проектиращ лъч Aa (фиг. 4.7) точката може да заема различни позиции, намирайки се над или под дадената точка A, и е невъзможно да се определи каква позиция на точката в пространството съответства на изображението (проекцията) a.
Ориз. 4.4. Ориз. 4.5. Ориз. 4.6.
За да се определи нейното положение в пространството от изображението на точка, е необходимо да има поне две проекции на тази точка. В този случай трябва да се знае взаимното разположение на проекционните равнини и посоката на проекцията. След това, имайки две изображения на точка А, ще бъде възможно да си представим как се намира точката в пространството.
Най-простият и удобен е проекцията върху взаимно перпендикулярни проекционни равнини с помощта на прожектиращи лъчи, перпендикулярни на проекционните равнини.
Тази проекция се нарича ортогонална проекция, а получените изображения се наричат ортогонални проекции.