Спектрален анализ на сигнали
Спектрален анализ на сигнали
Автор: admin от 18-03-2015, 18:46, прегледани: 2383
Не толкова отдавна другарят Макеман описа как чрез спектрален анализ може да се разложи определен звуков сигнал на съставните му ноти. Нека се абстрахираме малко от звука и приемем, че имаме някакъв цифровизиран сигнал, чийто спектрален състав искаме да определим и то доста точно.
В секцията, кратък преглед на метода за извличане на хармоници от произволен сигнал с помощта на цифрово хетеродиниране и малко специална магия на Фурие.
И така, какво имаме. Файл с проби от цифровизирания сигнал. Известно е, че сигналът е сбор от синусоиди с техните честоти, амплитуди и начални фази и, вероятно, бял шум.
Какво ще правим. Използвайте спектрален анализ, за да определите:
- броят на хармониците в сигнала и за всеки: амплитуда, честота (по-нататък в контекста на броя дължини на вълните на дължина на сигнала), начална фаза;
- наличие/отсъствие на бял шум и, ако има, неговото RMS (стандартно отклонение);
- наличие/отсъствие на постоянната съставка на сигнала;
- всичко това е поставено в красив PDF отчет с блекджек и илюстрации.
Ще решим този проблем в Java.
Както казах, структурата на сигнала е очевидно известна: това е сбор от синусоиди и някакъв вид шумов компонент. Така се случи, че за анализа на периодични сигнали в инженерната практика широко се използва мощен математически апарат, обикновено наричан"анализ на Фурие". Нека да разгледаме набързо какъв вид животно е.
Малко специално, магия на Фурие
Не толкова отдавна, през 19 век,Френският математик Жан Батист Жозеф Фурие показа, че всяка функция, която отговаря на определени условия (непрекъснатост във времето, периодичност, изпълнение на условията на Дирихле), може да бъде разширена в серия, която по-късно получава неговото име -ред на Фурие.
В инженерната практика разширението на периодични функции в серия на Фурие се използва широко, например, в проблемите на теорията на веригата: несинусоидално входно действие се разлага на сума от синусоидални и необходимите параметри на веригата се изчисляват, например, с помощта на метода на суперпозиция.
Има няколко възможни начина за записване на коефициентите на реда на Фурие, но ние просто трябва да знаем същността. Разширението в ред на Фурие ви позволява да разширите непрекъсната функция в сбор от други непрекъснати функции. И в общия случай поредицата ще има безкраен брой членове.
Допълнително подобрение на подхода на Фурие е интегралната трансформация на собственото му име.Преобразуване на Фурие. За разлика от реда на Фурие, преобразуването на Фурие разлага функцията не по отношение на дискретни честоти (наборът от честоти на реда на Фурие, в който се извършва разширението, е най-общо казано дискретно), а по отношение на непрекъснати. Нека да разгледаме как коефициентите на реда на Фурие и резултата от Фурие er трансформация, наречена всъщностспектър, корелат Малко отклонение: спектърът на трансформацията на Фурие е като цяло сложна функция, която описвакомплексни амплитудина съответните хармоници. Тоест стойностите на спектъра са комплексни числа, чиито модули са амплитудите на съответните честоти, а аргументите са съответните начални фази. На практикаамплитуден спектърифазов спектърсе разглеждат отделно.
Лесно е да се види, че коефициентите на серията на Фурие не са нищо повече от стойностите на преобразуването на Фурие в дискретни времена.
Преобразуването на Фурие обаче сравнява непрекъсната във времето, безкрайна функция с друга непрекъсната по честота, безкрайна функция – спектъра. Ами ако нямаме безкрайна във времето функция, а само някаква записана част от нея, дискретна във времето? Отговорът на този въпрос се дава от по-нататъшното развитие на трансформацията на Фурие -дискретна трансформация на Фурие (DFT).
Дискретното преобразуване на Фурие е предназначено да реши проблема с необходимостта от непрекъснатост и безкрайност във времето на сигнала. Всъщност ние вярваме, че изрязваме част от безкрайния сигнал и смятаме, че този сигнал е нула за останалата част от времевата област.
Математически това означава, че като функцията f(t) е безкрайна в изследваното време, ние я умножаваме по някаква прозоречна функция w(t), която изчезва навсякъде, с изключение на интервала от време, който ни интересува.
Ако "изходът" на класическото преобразуване на Фурие е спектърът - функция, тогава "изходът" на дискретното преобразуване на Фурие е дискретният спектър. И броят на дискретен сигнал също се подават на входа.
Останалите свойства на преобразуването на Фурие не се променят: можете да прочетете за тях в съответната литература.
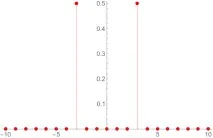
Трябва само да знаем за образа на Фурие на синусоидалния сигнал, който ще се опитаме да намерим в нашия спектър. Като цяло, това е двойка делта функции, които са симетрични относно нулевата честота в честотната област.
Вече споменах, че най-общо казано, разглеждаме не оригиналната функция, а част от нейнатапродукт с функция прозорец. Тогава, ако спектърът на оригиналната функция е F(w), а функцията на прозореца е W(w), тогава спектърът на продукта ще бъде такава неприятна операция като навиването на тези два спектъра (F * W) (w) (теорема за конволюцията).
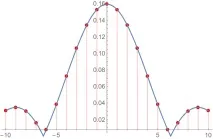
На практика това означава, че вместо делта функция ще видим нещо подобно в спектъра:
Този ефект се нарича ощеразпространяване на спектъра(на английски spectral leekage). И шумът, който се появява поради разпространението на спектъра, съответностранични лъчи(англ. sidelobes). Други, неправоъгълни функции на прозореца се използват за борба със страничните лобове. Основната характеристика на "ефективността" на функцията на прозореца енивото на страничния лист(dB). По-долу е показана обобщена таблица на нивата на страничния лист за някои често използвани функции на прозореца.
| функция прозорец | Ниво на страничния лист (dB) |
| Прозорец на Дирихле (правоъгълен прозорец) | -13 dB |
| прозорец Хана | -31,5 dB |
| Прозорец на Хеминг | -42 dB |
Основният проблем в нашата задача е, че страничните лобове могат да маскират други хармоници, разположени наблизо.
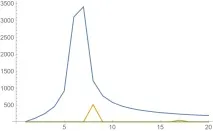
Може да се види, че при добавяне на намалените спектри, по-слабите хармоници изглежда се разтварят в по-силните.
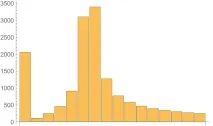
Друг подход за борба с разпространението на спектъра е да извадите от сигнала хармониците, които създават това разпространение. Това означава, че като зададете амплитудата, честотата и началната фаза на хармоника, можете да го извадите отсигнал, докато премахваме съответстващата му "делта функция", а с нея и генерираните от нея странични лобове. Друг е въпросът как точно да разберете параметрите на желания хармоник. Не е достатъчно просто да вземете желаните данни от комплексната амплитуда. Комплексните амплитуди на спектъра се формират от цели честоти, но нищо не пречи на хармоника да има частична честота. В този случай комплексната амплитуда изглежда се размива между две съседни честоти и точната й честота, подобно на други параметри, не може да бъде установена.
За да установим точната честота и комплексната амплитуда на желания хармоник, ще използваме техника, широко използвана в много отрасли на инженерната практика -хетеродин.
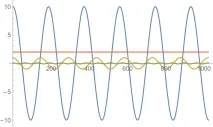
Нека да видим какво се случва, ако умножим входния сигнал по комплексния хармоник Exp(I*w*t). Спектърът на сигнала ще се измести с w надясно. Ние ще използваме това свойство, като изместим спектъра на нашия сигнал надясно, докато хармоникът стане още по-подобен на делта функция (тоест докато някое местно съотношение сигнал/шум достигне максимум). След това ще можем да изчислим точната честота на желания хармоник, като w0 - whet, и да я извадим от оригиналния сигнал, за да потиснем ефекта от разпространението на спектъра. По-долу е показана илюстрация на промяната на спектъра в зависимост от честотата на локалния осцилатор.
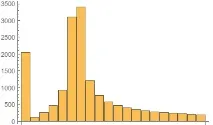
Ще повтаряме описаните процедури, докато изрежем всички налични хармоници и спектърът не ни напомня за спектъра на белия шум.
След това трябва да оценим RMS на белия шум. Тук няма трикове: можете просто да използвате формулата за изчисляване на RMS:
Автоматизирайте го
Време е да автоматизирате изборахармоници. Нека повторим алгоритъма още веднъж:
1. Търсим глобален пик на амплитудния спектър, над определен праг k. 1.1 Ако не бъде намерен, завършете 2. Чрез промяна на честотата на локалния осцилатор, ние търсим такава честотна стойност, при която максимумът на някакво локално съотношение сигнал/шум ще бъде постигнато в някаква близост до пика 3. Ако е необходимо, закръгляме стойностите на амплитудата и фазата. 4. Изваждаме от сигнала хармоник с намерената честота, амплитуда и фаза минус честотата на локалния осцилатор. 5. Да преминем към точка 1.
Алгоритъмът не е сложен и единственият въпрос, който възниква, е откъде да вземем праговите стойности, над които ще търсим хармоници? За да се отговори на този въпрос, трябва да се оцени нивото на шума дори преди да се изрежат хармоници.
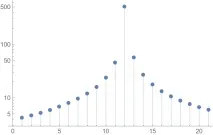
Нека изградим функция на разпределение (здравей, математическа статистика), където абсцисата ще бъде амплитудата на хармониците, а ординатата ще бъде броят на хармониците, които не надвишават същата стойност на аргумента по амплитуда. Пример за такава изградена функция:
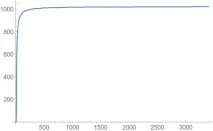
Сега нека изградим друга функция - плътността на разпределение. Тоест стойностите на крайните разлики от функцията на разпределение.
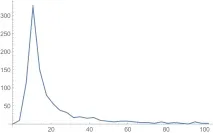
Абсцисата на максимума на плътността на разпределението е амплитудата на хармоника, която се появява в спектъра най-много пъти. Нека се отдалечим от пика вдясно за известно разстояние и ще разгледаме абсцисата на тази точка като оценка на нивото на шума в нашия спектър. Сега можете да автоматизирате.
Практическа част
Не претендирам да съм експерт по Java и представеното решение може да е съмнително както по отношение на производителността и консумацията на памет, така и като цяло философията на Java и OOP философията, колкото и да се опитвам да го направя по-добро. Беше написано заняколко вечери, като доказателство за концепцията. Тези, които се интересуват, могат да проверят изходния код на GitHub.
Единствената трудност беше генерирането на PDF отчет въз основа на резултатите от анализа: PDFbox не искаше да работи с кирилица по никакъв начин. Между другото, сега не иска.
Следните библиотеки бяха използвани в проекта: JFreeChart - показване на диаграми PDFBox - създаване на отчет JLatexMath - изобразяване на латекс формули
В резултат на това получихме доста масивна програма (13,6 мегабайта), която удобно изпълнява задачата.
Възможно е да изрежете хармониците ръчно или да поверите тази задача на алгоритъма.
Благодаря на всички за вниманието!
Литература
Sergienko A.B. — Цифрова обработка на сигнали