Статистиката и котките като топли котки станаха част от научна книга, списание Popular Mechanics

Описателна статистика: кои са котките
Тюлените са различни: големи и малки, с висящи уши и къси крака, с дълга опашка или изобщо без опашка. Но във всеки от тях има някои характеристики, които ни позволяват да ги обединим под общото наименование "тюлени". Но някъде има котка, която може да се счита за най-типичния представител на семейството. Как да го намерите? За простота нека вземем свойство като размер. Първото нещо, което можем да направим, е да видим какъв размер уплътнения са по-често срещани. Този размер се нарича мода и може да се твърди, че е най-типичният. Можем също така да подредим котките в ред, от най-малката до най-голямата, и да видим какъв размер е котката точно в средата. Този размер се нарича медиана.

Е, ако съберем размерите на всички наши котки и разделим на техния брой, получаваме средноаритметичното, познато ни от училище. Важно е да запомните, че средната стойност е много чувствителна към отклоненията. Ако в нашата извадка бъде включен екземпляр с размер на слон, тогава неговият размер значително ще измести средната стойност нагоре и тогава той вече няма да отразява реалната картина.

Мода, медиана и средна стойност ни позволяват да намерим типичните размери на уплътненията и се наричат мерки на централната тенденция. Но в допълнение към типичните стойности, ние също се интересуваме колко разнообразни могат да бъдат уплътненията. Мерките за променливост могат да ни помогнат с това. Най-простият от тях - span - е само разликата между най-големите и най-малките котки. Понякога статистиците отрязват 25% от най-големите и 25% от най-малките тюлени, като изчисляват разликата само за „средната“ група. Товастойността се нарича интерквартилен диапазон.

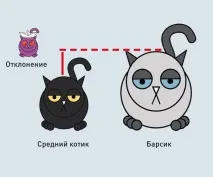
Дисперсията може също да бъде оценена с помощта на дисперсията. Да предположим, че решим да сравним размера на конкретен Barsik със средния размер на котка. Разликата (или по-скоро разликата) на тези размери се нарича отклонение от средната стойност. Колкото повече Барсик се различава от него, толкова по-голямо е отклонението. И разбира се, колкото повече примери с голямо отклонение, толкова по-разнообразни са уплътненията по размер.
Тест по математика: можете ли да го издържите?
Как бързо да изчислите процентите наум: математически трик
За да оценим разнообразието, можем да продължим по вече изпитания начин: да съберем всички отклонения и да разделим на общия брой уплътнения, тоест да намерим средната стойност на отклоненията. Но тъй като отклоненията могат да бъдат както положителни, така и отрицателни, тяхната сума ще ни даде нула. За да не се случи това, статистиците повдигат отклоненията на квадрат и едва тогава намират средната стойност. Получената стойност се нарича дисперсия (D). Дисперсията обаче не е много удобна за оценка на разнообразието от тюлени, тъй като размерът се измерва в обикновени сантиметри, а дисперсията се измерва в квадратни метри. Следователно, за удобство, се взема корен от дисперсията, като се получава стандартното отклонение (S).

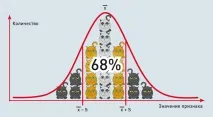
Средната стойност и стандартното отклонение често се използват заедно за компактно описание на определена група тюлени. Като правило, по-голямата част (около 68%) от котките са в рамките на едно стандартно отклонение от средната стойност. Тези котки са с нормален размер. Останалите 32% са или много големи, или много малки котки.
Всичко, за което говорихме по-горе, се отнася до описателна статистика, чиято задача е да даде кратка представа за това как изглеждат изследваните обекти.ни обекти. Централната мярка на тенденцията показва как изглежда най-типичният от тях. Мярката за променливост отразява тяхното разнообразие. Но в допълнение към описателните, има много по-обширен клас методи, които ни позволяват да тестваме хипотези, свързани с нашите обекти. И тук на помощ на котките идват ... кучетата.
Статистика, базирана на доказателства: как котките се различават от кучетата
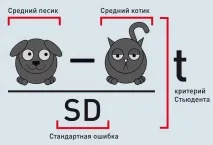
В някои отношения кучетата и котките си приличат: и двете имат четири лапи, опашка и чифт уши, но се различават по много начини. Може би има разлика в размера, но как да проверя това? В крайна сметка има както много малки кучета, така и много големи котки ... Първото нещо, което идва на ум, е да се изчисли средният размер на тюлените и средният размер на кучетата и след това да се извади един от друг: колкото по-голяма е тази стойност, толкова по-голяма е разликата между тях. Статистиците правят това, като разделят тази разлика на стандартната грешка, фактор, който зависи от размера на извадката и дисперсията. Полученият резултат се нарича t-тест на Student. И колкото по-голям е t-тестът, толкова по-уверени можем да кажем, че средно кучетата се различават от тюлените по размер.
Но колко голям трябва да бъде t-тестът на Стюдънт, за да можем уверено да говорим за разликата в размерите на кучетата и тюлените? За да разрешат тази трудност, статистиците тръгват от обратното, излагайки нулева хипотеза. Нека направим това и приемем, че средните размери на тюлените и кучетата са еднакви. Сега остава да видим с каква вероятност ще получим същата (или по-голяма) стойност на t-теста, ако нулевата хипотеза е вярна. Тази вероятност се нарича ниво на р-значимост и ако е голямо (по-голямо от 5% или 0,05), тогава нулевата хипотеза не се отхвърля. Ако p-нивото е ниско (по-малко от 5% - 0,05), тогава нулевата хипотезаалтернативата се отхвърля и приема - че тюлените все пак са различни от кучетата. Поне като размер.

Напоследък p-стойността е често критикувана, но тя продължава да бъде една от основните концепции на базираната на доказателства статистика. Независимо дали търсите разлики между котки и кучета или намирате връзки между храненето и размера на котката, вие непременно ще срещнете тази концепция.
И така, базираната на доказателства статистика ви позволява да тествате хипотези за света около вас. Заедно с описателния, той решава огромен брой научни и практически проблеми в различни области, от психология и генетика до производство и маркетинг. Той далеч не се ограничава до концепциите, обсъдени в тази статия. Изучавайте статистики и обичайте котките.