Функционална граница, функционална граница
Функция y=f(x) се нарича ограничена върху някакво множество M от стойности на аргумента x, ако съществува положително число С, такова че за всички x$\in $M е валидно следното неравенство:
Такова множество може да бъде например интервал, сегмент или цялата числова линия.
Функцията y=sin(x) е ограничена на цялата числова линия, тъй като за всяка стойност на x имаме $ sin x≤ 1$.
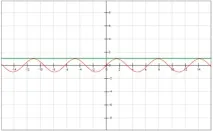
Фигура 1. Ограничена функция
Функцията y = x3 + 4 е ограничена на сегмента [0, 3], тъй като за всички x, принадлежащи на този сегмент, е валидно следното неравенство:
Това неравенство се получава чрез заместване на числото 3 вместо функцията x:
y=33+4=27+4=31
Функцията $y=\frac $ ограничена ли е в интервала (0, 1)?
Отговор: Тъй като е невъзможно да се определи число C, така че за всички x$\in $(0,1) е валидно следното неравенство:
Функцията не е ограничена.
Опитайте да помолите учителите за помощ.
Ако функция y=f(x) има граница при $x\to +\infty$, тогава тя е ограничена в някакъв безкраен интервал $(N,+ \infty)$.
Тогава, според дефиницията на границата, за $\varepsilon $ = 1 имаме
\[\съществува N\mathop\limits_ (x>N)\Rightarrow \leftf(x)-b\right върху безкрайния интервал $(N,+ \infty)$.
За функция, ограничена в безкраен интервал $(N,+ \infty)$, се казва, че е ограничена като $x\to +\infty$.
Ако функцията y=f(x) има ненулева граница (за $x\to +\infty$), тогава функцията
ограничен (на някакъв безкраен интервал).
Задай въпросексперти и получете отговор за 15 минути!
И нека $\varepsilon \[\exists N\mathop\limits_ (x>N)\Rightarrow \leftf(x)-b\right е положително число, тъй като:
$\leftf(x)-b\right=\leftb-f(x)\right\ge \leftb\right-\leftf(x)\right$ след това $\leftb\right-\leftf(x)\right\leftb\right-\varepsilon >0$
Все още не сте намерили отговора на въпроса си?
Просто напишете за какво имате нужда от помощ