Относно приложението на статично адаптивно разделяне на изчислителната област, Simmakers Blog
Въведение
Много софтуерни пакети за числени изчисления предоставят на потребителите възможността да използват статична адаптивна (наричана по-нататък просто адаптивна) стъпка при конструиране на ортогонална хексаедрична структурирана изчислителна мрежа. Тоест, въз основа на собствения си опит, потребителят, който желае да получи по-точно изчисление и в същото време да не увеличава значително времето за изчисление, може да посочи на такива програми онези места в изчислителната област, където според него е необходимо да се приложи по-подробно разделяне (използвайте по-малка стъпка в пространството) в сравнение с останалата част от изчислителната област.
Когато се прилага правилно, статичното адаптивно разделяне на изчислителната област е мощен инструмент в числените изчисления, повишавайки тяхната точност. Въпреки това, ако се злоупотребява с описаната по-горе опция, времето за изчисление може да се увеличи значително и точността на изчислението няма да се промени значително. В тази статия представяме теоретичните предимства и недостатъци на използването на адаптивното разделяне на изчислителната област и също така даваме два примера за числени изчисления на термичните полета в почвата. В първия пример използването на адаптивна стъпка е подходящо, но във втория не е.
Недостатъци на използването на адаптивна мрежа
При численото решаване на нестационарни задачи времевата стъпка се избира от критерия за устойчивост на числената схема. Например, за численото решение на задачата за топлопроводимост чрез приближението на крайната разлика, критерият за избор на времева стъпка има формата:
където са минималните стъпки на пространството по осите, съответно, и константатаCсе избира въз основа на физическите параметри на проблема.
INВ случай на адаптивно разделяне на изчислителната област трябва да се избягва силно намаляване на пространствената стъпка във всяка посока в близост до един възел. Тъй като силното намаляване на стъпката в близост до един възел няма да доведе до забележимо увеличение на точността на изчислението като цяло, но, както следва от формула (1), значително ще намали стъпката във времето, което означава, че времето за изчисление ще се увеличи.
Отделно си струва да споменем проблема с използването на адаптивна мрежа за апроксимация с крайни разлики на диференциални оператори. Проблемът е, че редът на приближение на диференциалните оператори обикновено пада. Помислете например за апроксимация с крайни разлики на оператора . Прилагайки приближението върху стандартния шаблон, получаваме следната формула:
Където . Приемайки достатъчна гладкост на функциятаu, базирана на формулата на Тейлър, имаме следните равенства:
Замествайки равенства (3) и (4) в (2) и привеждайки подобни членове, получаваме отношението:
От формула (5) следва, че за , операторът се апроксимира с първи ред на точност. В същото време на правилна мрежа и операторът се апроксимира с втори ред на точност.
Плюсовете на използването на адаптивна мрежа
Въпреки факта, че в общия случай диференциалният оператор се апроксимира с първи ред на точност, на практика, ако и не се различават значително, тогава членът в (5) ще бъде доста малък и няма да има голям ефект върху точността на апроксимацията.
Също така си струва да се отбележи, че ако потребителят желае да получи по-точно решение в малка област, тогава има смисъл да се прецизира мрежата само в тази област, вместо да се прецизира мрежата в цялата изчислителна област. В такъв случай използвайтеадаптивната мрежа може значително да намали броя на възлите на мрежата, като по този начин значително намали времето за изчисление и количеството използвана памет.
Необходимостта от използване на адаптивна мрежа възниква, когато е необходимо да се получи детайлна дискретизация на малки обекти със сложна форма. Използването на еднаква мрежа в такива случаи води до прекомерно увеличаване на броя на възлите, което усложнява както изграждането на модел за изчисление, така и по-нататъшното изчисление върху него.
Сравнение на резултатите от изчисленията
Пример 1
Използвайки софтуерния пакет Frost 3D, ще симулираме проблема с топлопроводимостта с фазови преходи. Изгледът отгоре на компилирания модел е показан на фигура 1:
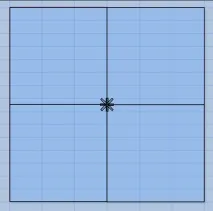
Фигура 1 – Изглед отгоре на изчислителната област
Изчислителната област съдържа четири паралелепипеда и особеност под формата на звездичка в центъра. Ширината и височината на изчислителната област са 60 м, височината е 20 м. Физическите параметри на материалите са дадени в таблица 1.
Таблица 1 - Физически параметри на материалите