Постоянна опашка и нейните приятели

Преди известно време се натъкнах на постоянни структури от данни и по-специално на описанието на постоянна опашка в wiki бележките на ITMO. Всичко би било наред, само по някакъв начин сложно: за реализиране на една малка опашка се използват пет (в друга версия шест) стека.

Ще припомня накратко историята на проблема, ще се побера само в четири стека и в същото време ще ви разкажа малко за постоянството като цяло.

Упоритост

Устойчивостта на структура от данни е способността да се съхраняват множество версии наведнъж. С други думи, всяка модифицираща операция (например структурата от данни „stack“ има операциитеpush иpop ) не променя самата структура, а връща нова структура от данни (обикновено под формата на връзка към новата версия), която съхранява това, което е трябвало да се появи в старата след тази операция. Това е еквивалентно на факта, че можете (бързо) да копирате цялата структура на данните и след това да извършвате всякакви операции.

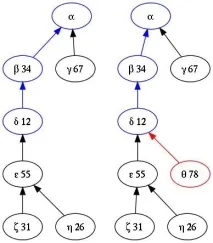
Фигурата показва пример за постоянен стек преди и след операцията θ = push (δ, 78) . Гръцките букви обозначават версии на стека, например версияη съответства на стек с елементи 34, 12, 55, 26, аα е празен стек. В процеса на работа със стека могат да се появят нови върхове, но старите нито ще изчезнат, нито ще се променят, това е смисълът на постоянството.

По подобен начин можете да поддържате други структури от данни, които са представени като малки структури с ациклични връзки: двоични дървета, дърво на сегменти в изпълнение отгоре надолу. В случай на двоични дървета, обикновено при заявка се появява не един нов връх, а няколко наведнъж, защото трябва да се създадат нови версии за засегнатите върхове и за тези, които са ималивсички потомци са засегнати.

Сръчността на лапите и сегментното дърво ни позволяват да създадем структура от данни за „постоянен масив“ с операциите „увеличаване на дължината на масива с едно“ и „промяна на елемента“, но всяка такава операция ще бъде извършена в O (log) (логаритъм от дължината на масива). Тъй като всяка структура от данни може да бъде представена като промяна в някои стойности в масив, изглежда, че всяка структура от данни може да бъде запазена с добавянето на допълнително O (log) в асимптотиката. Не всичко обаче е толкова просто (това обаче ви позволява да направите постоянна опашка с O (дневник) на операция от опашката на масива).

Постоянна опашка

Както знаете, опашката е лесна за изпълнение с помощта на два стека: ние вземаме елементи от един, поставяме ги в друг, ако е необходимо, вземаме и прехвърляме всички елементи от втория към първия. Замяната на двата стека с постоянни води до постоянна опашка, така че защо има проблем с шест стека в абстрактна статия на wiki? Факт е, че е възможно да се приложи опашка през два стека, това ще даде оценка O (1) за операцията, но тази оценка се амортизира. И постоянството, за съжаление, не запазва амортизирани оценки.

Наистина, нека опашката на версияξ има първия стек празен и по време на следващата операцияget (по-нататък ще наричам операцията „поставяне на елемент в опашката“ катоput, „вземане от опашката“ -get ) ще трябва да прехвърли елементи в O(n) , къдетоn е броят на тези елементи. В нормална опашка тази операция ще бъде изпълнена и следващитеnget операции ще бъдат изпълнени лесно и естествено за чиста единица. Но в постоянния случай може да се наложи опашката да направи нещо друго със съхранената версияξ - и всяка такава операция ще бъде изпълнена в O(n). Провал.

Всъщност са необходими купчини с пет или шест стека, за да се изгради опашка, която, от една страна, се основава на стекове, от друга страна, изпълнява операции за истински O (1) , а не за амортизирани, тоест опитва се да прехвърли елементи от втория стек към първия предварително, един по един, чрез няколко спомагателни. Такава опашка вече е лесно устойчива. Но започнах с факта, че пет (особено шест) стака е малко сложно и сега ще се опитам да мина с четири.

Четири стека

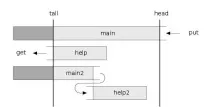
Първият стек (main ) просто ще съхранява всички елементи, които някога са били добавяни към опашката. Операциятаput ще добави елемент къмmain (и след това ще преизчисли някои броячи и ще направи нещо).

Вторият стек (help ) ще съхранява някои действителни елементи в обратен ред, така че елементите винаги да могат да бъдат взети от него за операциятаget. Тоест операциятаget ще вземе елемент отhelp (а също така ще преизчисли и направи нещо).

За да предотвратим вземането на елементите от нищото, имаме нужда от още един стек (help2 ). Той ще съдържа някои елементи от опашката, ще расте и когатоhelp приключи (или по-рано), ще дойде да го замени.

За да увеличим стекаhelp2, имаме нужда (внимание) от постоянно копие на стекаmain, от който ще вземем елементи и ще прехвърлим елементи къмhelp2. Това копие се наричаmain2.

Всичко изглежда така:

Действието, което нарекох нещо, е насищането на стекаhelp2 и затова трябва да съхраним няколко брояча. Достатъчно е да знаете броя на елементите в опашката (нека се казваmain_size, въпреки че всъщностmain също съхранява остарели елементи) и броя на елементите, които оставатхвърляне към спомагателния стек (съответно,main2_size ). Операциятаput прави main_size++ и не докосваmain2_size, операциятаget прави main_size--, main2_size-- .

Е, нещо трябва да прави следното:

Ако main2_size > 0, след това преместете един елемент отmain2 къмhelp2 и main2_size--

Ако main2_size == 0, тогава заменетеhelp сhelp2 и заменетеhelp2 иmain2 с празни стекове

Акоhelp2 е празно, тогава копирайтеmain вmain2 (за O(1), постоянният стек поддържа това между другото) и задайте main2_size = main_size.

Също така трябва да се докаже, че няма да има ситуация, при която опашката да не е празна и стекътhelp да е празен, но ще оставя това на читателя. В моя VKontakte публикувах кода, който получих по тази тема.

Знам два недостатъка на такава реализация в сравнение с петте стека, които са в бележките на wiki. И двете възникнаха поради факта, чеосновният стек съхранява като цяло всички елементи, които са били добавени към опашката, а не само тези, които са останали в опашката в текущия момент.

Първият недостатък е използването на паметта. Ако има информация отвън, че не трябва да се използват всички версии, а само някои конкретни, тогава можете да събирате боклук и да спестите памет. При мен старите елементи ще висят на опашкатаmain.

Второто минус е, че е по-трудно да се свърже някаква допълнителна функция, например изчисляване на минимума върху текущите елементи на опашката. Възможно е, но ще ви трябват още няколко стека за поддръжка.