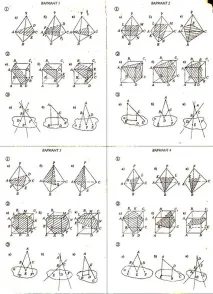
Построяване на сечения на тетраедър и паралелепипед”, Платформа за съдържание

MOU Starskaya средно училище
по геометрия в 10 клас на тема:
"Построяване на сечения на тетраедър и паралелепипед".
„Построяване на сечения на тетраедър и паралелепипед“
1. Запознайте се с основите на решаването на задачи за построяване на сечения на тетраедър и паралелепипед с равнина.
2. Изберете типове задачи за построяване на раздели.
3. Развийте умения за решаване на задачи за конструиране на сечения на тетраедър и паралелепипед.
4. Формиране на пространствено въображение.
I организационен момент.
II Проверка на домашните.
Момчета, какви геометрични тела изучавахме в последните уроци? (тетраедър, паралелепипед).
Какво е тетраедър?
Какво е паралелепипед?
Сега нека проверим устната си домашна работа.
В учебника на стр. 31 четем и отговаряме на въпроси 14,15.
14.Има ли тетраедър с пет прави ъгъла?
(Не, защото в четирите триъгълника, които се образуват, може да има само четири прави ъгъла, не повече по един във всеки).
15.Има ли кутия с:
a) Само едно лице е правоъгълник. (Не, тъй като срещуположните страни на кутията са равни).
b) Само две съседни диамантени лица. (Не, само срещуположните лица могат да бъдат ромби).
v) Всички ъгли на лицето са остри. (Не, успоредникът има както остри, така и тъпи ъгли и всяко лице на успоредник).
r) Всички ъгли на лицето са прави. (Да, в кубоид).
e) Броят на всички остри ъгли на лицето не е равен на броявсички тъпи ъгли на лицето. (Не, острите и тъпите ъгли са равни във всяко лице).
III Обяснение на новата тема.
Сега да преминем към нова тема. Запишете темата на урока. Целта на днешния урок:
1. Запознайте се с основите на решаването на задачи за построяване на сечения на тетраедър и паралелепипед с равнина.
2. Изберете видовете задачи за изграждане на раздели.
3. Развийте умения за решаване на проблеми за конструиране на сечения на тетраедър и паралелепипед.
4. Формиране на пространствено въображение.
Така че за решаването на много геометрични проблеми, свързани с тетраедър и паралелепипед, е полезно да можете да изграждате техните секции във фигурата от различни равнини.
Какво имаме предвид подсечеща равнина? В учебника на стр. 27 ще намерим отговора на този въпрос.
Сечеща равнинае всяка равнина, от двете страни на която има точки на даден полиедър.
Следващата концепция ераздел.И отново се обръщаме към учебника за помощ. Сега вижте как изглежда точната дефиниция на секцията.
v Къде са страните на многоъгълник, който е сечение?
v Къде са върховете на многоъгълника, който е разположен секцията?
А сега да отговорим на въпроса.Какво означава да построим сечение на многостен с равнина.Така във всяко лице ще построим сегменти, по които сечащата равнина пресича лицата.
За да се изгради правилно разрез, човек трябва да може да прилага различни теореми и свойства. Да отговорим на въпроса.
Кои от тези твърдения могат да бъдат полезни при конструирането на секции?
1. Ако две равнини имат обща точка, тогава те се пресичат по правата, съдържаща тази точка.
2. Ако прав,лежаща в една от пресичащите се равнини, пресича друга равнина, след което пресича линията на пресичане на равнините.
3. Ако две успоредни равнини са пресечени от трета, тогава пресечните линии на равнините са успоредни.
4. Секущата равнина пресича лицето на полиедъра по начупена линия.
5. В разрез на паралелепипед от равнина може да се окаже:
А сега нека си припомним как да настроим самолета:
При конструирането на секции е важно да знаете:




Сега в учебника ще разгледаме основните задачи за конструиране на раздели. И така, първата задача, където е необходимо да се построи сечение на тетраедър от три точки, принадлежащи на секуща равнина, две от които лежат в една равнина, а третата лежи в друга равнина.


Решениетона задача 2ще бъде разгледано в учебника по фиг.41.
Построете сечение на тетраедъра с равнина, минаваща през точка M, лежаща в лицето ADB, успоредна на основата ABC.
Тъй като сечащата равнина е успоредна на равнината ABC, тя е успоредна на правите AB, BC, AC. Следователно сечащата равнина пресича страничните стени на тетраедъра по правите линии, успоредни на страните на триъгълника ABC.
Построете сечение на паралелепипед с равнина, минаваща през точки A, B, C.
Този проблем има няколко решения, които зависят от разположението на точките върху повърхността на тетраедъра. На стр. 27 от учебника ще видите как можете да построите сечение на паралелепипед.
В някои ситуации се използва свойството за успоредност на противоположните лица на паралелепипеда. Те се пресичат от сечащата равнина по успоредни прави. А сега предлагам на вашето внимание няколко задачи:
IV Затвърдяване на нова тема.
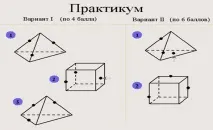
Решаване на проблеми. Проверка на правилността на решението с помощта на слайдове.
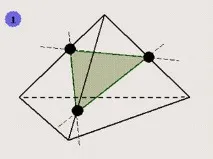
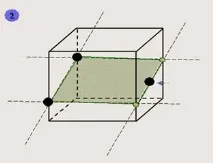
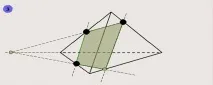
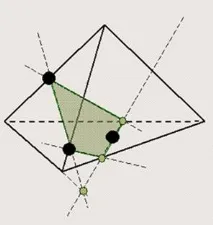
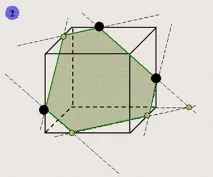

За да изградите допълнителни точки, принадлежащи към него, е удобно да използвате следния шаблон.
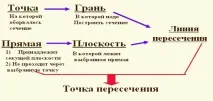
И сега отивам да тествам. Трябва да изпълните три задачи в рамките на три минути. Изберете и запишете броя на рисунките, които показват правилните сечения на тетраедъра и паралелепипеда, както и правилния чертеж.