Течности, възникващи върху извита повърхност
Течността се характеризира с извита повърхност, тъй като за да

повърхността на течността е била плоска, е необходимо действието на външна сила - силата на гравитацията или силата на взаимодействие с повърхността (разпръскване).
Помислете за сферична частица. Поради силите на повърхностното напрежение обемът му може да се промени.
Работата на компресията dA е
Намаляването на повърхностната енергия
където dS е намалението на повърхността на топката, съответстващо на намаляването на радиуса с dr. от
известни формули за повърхността S = 4πr 2 и обема на топката и V = 4/3 πr 3 получаваме очевидните изрази:
dS= 8πr, V = 4πr 2
Замествайки тези стойности за dS и dV в уравненията и като вземем предвид, че dA = dF, получаваме:
откъдето за налягането, упражнявано върху течността от нейната извита повърхност, се получава следният израз:
(1) Ако повърхността на течността не е сферична, а цилиндрична, тогава допълнителното налягане, причинено от кривината, се дава от
(2) В общия случай на повърхност с произволна форма (не сферична, не цилиндрична), налягането, дължащо се на кривината на повърхността, се изразява с уравнение, известно като уравнение на Лаплас:
където r 1 и r 2 са главните радиуси на кривина в дадена точка на повърхността или по-точно за даден повърхностен елемент.
За една сфера двата главни радиуса на кривина съвпадат и са равни на радиуса на сферата, т.е. r1=r1=r, и
(3) влиза в (1). За цилиндър един от основните радиуси на кривина е равен на ∞, а другият съвпада с радиуса на цилиндъра; Допълнителният натиск, определен по формулата на Лаплас, е насочен към центъра на кривината
повърхности. Следователно, в случай на изпъкнала повърхност, тя е насочена вътре в течността идобавя към нормалното налягане на течността. В случай на вдлъбната повърхност, течността ще бъде под налягане, по-малко от същата течност под плоска повърхност. Математически това съответства на факта, че радиусът на кривина за вдлъбната повърхност, когато центърът на кривина е извън течността, се счита за отрицателен, а за изпъкнала повърхност - за положителен.
Трябва да се помни, че допълнителното налягане, създадено от кривината на повърхността и определено от уравнение (3), не може да бъде идентифицирано с повърхностни сили, които са насочени тангенциално към повърхността, докато допълнителното налягане на Лаплас е насочено перпендикулярно на нея. Възниква само в резултат на действието на силите
повърхностно напрежение, което изкривява повърхността на течността.
10.9 Капилярни явления
Когато течността е в тесен съд, влиянието на стените се простира върху цялата повърхност на течността и тя се оказва извита по цялата си дължина (съдът може да се счита за тесен, когато размерите му са сравними с радиуса на кривината на повърхността на течността в контакт със стените на съда).
Ако размерите на съда, в който се намира течността, или по-общо, ако разстоянието между повърхностите, които свързват течността, са сравними с радиуса на кривината на повърхността на течността, тогава такива съдове се наричат капилярни (космати). Явленията, възникващи в такива съдове, се наричат капилярни явления.
Тъй като капилярните съдове се характеризират предимно с кривината на повърхността на течността в тях, естествено е ефектът от допълнителното налягане, причинено от кривината на повърхността (налягане на Лаплас), да е най-силно изразен тук. Непосредствената последица от това допълнително налягане е така нареченото капилярно покачване.
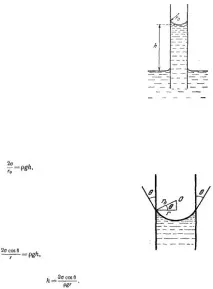
Наориз. е показана тясна тръба, спусната в широк съд с течност.
Оставете стените на тръбата да се намокрят с течност. Тогава течността, която е проникнала в тръбата, образува вдлъбнат менискус. Нека тръбата е толкова тясна, че нейният радиус r е сравним с радиуса r 0 на менискуса.
Поради налягането, причинено от кривината на повърхността, течността, изпълваща тръбата, изпитва налягане p, насочено към центъра на кривината на менискуса, т.е.
нагоре и равно на 2 σ/ r 0 , където r 0 на менискуса и σ е коефициентът на повърхността
Под действието на това налягане течността се издига през тръбата
до ниво h, при което хидростатичното налягане ρgh на течен стълб с височина h балансира налягането p. Условието за равновесие ще бъде равенство
Това равенство определя височината на издигане на течността в капиляра. Лесно е да се установи връзка между височината на повдигане h и радиуса на тръбата r. За това нека се обърнем към фиг., На която менискусът и капилярът са показани в голям мащаб. Центърът на сферата, част от която е менискусът, е в точка О. Контактният ъгъл на течността в контакт със стените на капиляра е θ. Пряко от чертежа следва, че r 0 = r/cosθ. Следователно горното уравнение ще бъде пренаписано във формата:
По-специално, за течност, която напълно намокря капилярните стени и за която θ=0 и cosθ = 1, имаме:
Както се очаква, височината на издигане на течността в капиляра (капилярно издигане) се увеличава с намаляване на радиуса на капиляра и с увеличаване на коефициента на повърхностно напрежение на течността.
Ако течността не намокри капиляра, картината ще бъде обърната, тъй като менискусът вече е изпъкнал и центърът на кривината не е извън, а вътре в течността и налягането на Лаплас ще бъде насочено надолу. Нивото на течността в капиляра сега ще бъде по-ниско от нивото в съда, в койтопонижен капиляр (отрицателно капилярно покачване).
Капилярното издигане обяснява редица добре известни явления: абсорбцията на течност от филтърна хартия, която е направена така, че да има тесни извити пори; пренасянето на керосин по фитила, чиито влакна също са тънки капиляри и др. Капилярните сили също осигуряват издигането на вода от почвата по стволовете на дърветата: дървесните влакна играят ролята на много тънки капиляри.
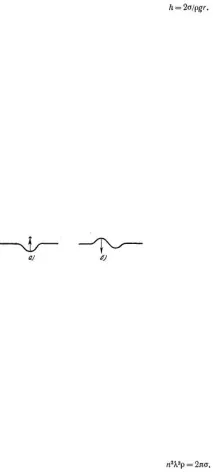
Капилярните вълни са другото име на добре познатия феномен на "вълнички" на повърхността на течност. Тези вълни се образуват под въздействието на малки смущения и възникването им е свързано със силите на повърхностно напрежение. Механизмът на образуване на капилярни вълни в общи линии е следният. Под въздействието на определени външни въздействия, повърхността на течността на дадено място се "натиска", ставайки вдлъбната
Налягането върху течните слоеве под тази вдлъбната повърхност става по-малко (с количеството σ/r) от налягането в съседните слоеве, където повърхността е останала плоска. Получената разлика в налягането кара течността от съседните слоеве да тече под вдлъбнатата повърхност и течността отново се издига до първоначалното ниво, но го преминава по инерция поради натрупаната кинетична енергия. Следователно повърхността ще стане изпъкнала и натискът, дължащ се на кривината на повърхността, ще бъде насочен надолу.
Ясно е, че такива трептения на течността на едно място ще накарат съседни точки да извършват същите трептения. Това означава, че явлението има вълнов характер. Капилярните вълни се отличават с малка амплитуда и къса дължина на вълната. Ако амплитудата е малка, ефектът на гравитацията може да бъде пренебрегнат, което може да причини същия ефект. (стръмните морски вълни дължат произхода си на гравитацията).
Вълнисамо в тези случаи те се наричат капилярни, когато в тяхното образуване участват само сили на повърхностно напрежение и те се образуват поради значителна кривина на върха и падината на вълната.
Изчислението показва, че параметрите на капилярните вълни са свързани с коефициента на повърхностно напрежение чрез следното уравнение:
където n е честотата на трептене във вълната, λ е дължината на вълната и ρ е плътността на течността. Формулата може да се използва за определяне на повърхностното напрежение на течност, чиято плътност е известна. За да направите това, е необходимо да измерите честотата на трептенията и дължината на вълната. Обикновено се измерва скоростта на разпространение на вълните, с която честотата