Графични трансформации: паралелна транслация, симетрия
3.1.5. Графични трансформации: паралелна транслация, симетрия спрямо координатните оси
Графични трансформации: паралелна транслация, симетрия
В чист вид основните елементарни функции, за съжаление, не са толкова често срещани. Много по-често се налага да се работи с елементарни функции, получени от основни елементарни функции чрез добавяне на константи и коефициенти. Графиките на такива функции могат да бъдат построени чрез прилагане на геометрични трансформации към графиките на съответните основни елементарни функции (или чрез преминаване към нова координатна система).
Използвайки геометрични трансформации на графиката на функцията f(x), може да се начертае всяка функция от вида \( \pm \cdot f( \pm \cdot (x + a)) + b,\), където \(, > 0\) са коефициентите на компресия или разширение (в зависимост от техните стойности) съответно по осите oy и ox. Знаците минус пред коефициентите показват симетричното изобразяване на графиката спрямо координатните оси, а и b определят изместването съответно спрямо абсцисната и ординатната ос.
По този начин има три вида геометрични трансформации на функционалната графика:
1. Първият изглед -мащабиране (свиване или разтягане) по абсцисната и ординатната ос.
Необходимостта от мащабиране се обозначава с коефициенти k1 и k2, които са различни от единица, ако \(0 1\) , тогава се разтягаме по ординатната ос и свиваме по абсцисната ос.
2. Вторият вид -симетричен (огледален) дисплей относно координатните оси.
Необходимостта от тази трансформация се обозначава със знаците минус пред коефициентите k1 (в този случай показваме графиката симетрично по отношение на оста ox) и k2 (в този случай показваме графиката симетрично по отношение на оста y). Ако няма знаци минус, тогава тази стъпкапропуснати.
3. Трети изглед -паралелен превод (изместване) по осите ox и oy.
Тази трансформация се извършвапоследнопри наличие на ненулеви коефициенти a и b. Ако a е положително, графиката се измества наляво с a единици; ако a е отрицателно, графиката се измества надясно с a единици. Ако b е положително, преместваме графиката на функцията успоредно нагоре с b единици, ако b е отрицателно - надолу с b единици.
Нека да разгледаме някои примери
Постройте графики на функцията \(y = - 10\) и \(y = + 10\) в една и съща координатна равнина.
Първо, нека изградим графика на функцията \(y = \) , това е парабола с връх в точката (0; 0) и се разклонява нагоре.
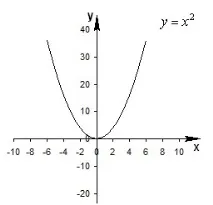
За да се построи търсената графика на функцията \(y = - 10\), е необходимо параболата да се движи успоредно в отрицателна посока по Y, т.е. надолу. За да се построи търсената графика на функцията \(y = + 10\), е необходимо параболата да се движи успоредно в положителна посока по Y, т.е. нагоре.
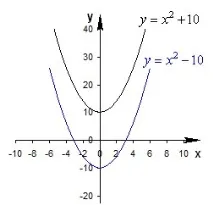
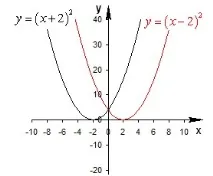
Начертайте функциите \(y = \right)^2>\) и \(y = \right)^2>\) .
Вземаме същата графика на парабола като основа, но ще извършим паралелен трансфер по оста Ox. Съгласно правилото за прехвърляне, графиката ще се измести наляво с 2 единици за функцията \(y = \right)^2>\) . А за функцията \(y = \right)^2>\) изместването ще бъде надясно.
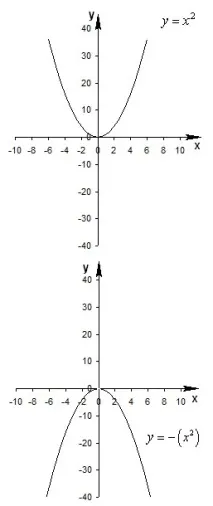
Начертайте функцията \(y = - \) .
За основа вземаме същата графика на парабола. Промяната в графиката се нарича -mapping. Картината ще се окаже симетрична на оригиналната парабола, симетрия по отношение на Ox.
Начертайте функциите \(y = \left( > \right)\) и \(y = \left( > \right)\) .
За да изградим тези графики, ще компресираме графиката \(y = \) за първата функция и ще я разтегнем за втората.