Стандартно отклонение, Коефициент на вариация
Корен квадратен от дисперсията се нарича стандартно отклонение от средната стойност, което се изчислява, както следва:
Елементарна алгебрична трансформация на формулата за стандартно отклонение я довежда до следния вид:
Тази формула често е по-удобна в практиката на изчисленията.
Стандартното отклонение, както и средното линейно отклонение, показва доколко специфичните стойности на атрибута се отклоняват средно от тяхната средна стойност. Стандартното отклонение винаги е по-голямо от средното линейно отклонение. Между тях има връзка:
Познавайки това съотношение, е възможно да се определи неизвестното от известните показатели, например, но(Iизчислявам и обратно. Стандартното отклонение измерва абсолютния размер на характеристичното колебание и се изразява в същите единици като характеристичните стойности (рубли, тонове, години и т.н.). Това е абсолютна мярка за вариация.
Заалтернативни характеристики,например наличието или отсъствието на висше образование, осигуровка, дисперсия и формулите за стандартно отклонение са:
Ще покажем изчисляването на стандартното отклонение според данните от дискретна серия, характеризираща разпределението на студентите от един от факултетите на университета по възраст (Таблица 6.2).
Таблица 6.2.Разпределение на учениците по възраст
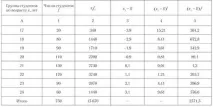
Резултатите от спомагателните изчисления са дадени в колони 2-5 на табл. 6.2.
Средната възраст на ученика, години, се определя по формулата за средноаритметично претеглено (колона 2):
В колони 3-4 се съдържат квадратите на отклонението на индивидуалната възраст на ученика от средната, а произведенията на квадратите на отклоненията отсъответните честоти са в колона 5.
Дисперсията на възрастта на учениците, години, намираме по формулата (6.2):
Тогава o \u003d l / 3,43 1,85 * oda, т.е. всяка конкретна стойност на възрастта на ученика се отклонява от средната стойност с 1,85 години.
Коефициентът на вариация
В своята абсолютна стойност стандартното отклонение зависи не само от степента на вариация на признака, но и от абсолютните нива на вариантите и средната стойност. Поради това е невъзможно директно да се сравнят стандартните отклонения на вариационни серии с различни средни нива. За да можете да направите такова сравнение, трябва да намерите дела на средното отклонение (линейно или квадратично) в средноаритметичното, изразено като процент, т.е. изчисляване наотносителни нива на вариация.
Линеен коефициент на вариацияизчислен по формулата
Коефициентът на вариациясе определя по следната формула:
В коефициентите на вариация се елиминира не само несъвместимостта, свързана с различните мерни единици на изследваната черта, но и несъвместимостта, произтичаща от разликите в стойността на средните аритметични стойности. В допълнение, показателите за вариация дават характеристика на хомогенността на съвкупността. Наборът се счита за хомогенен, ако коефициентът на вариация не надвишава 33%.
Според табл. 6.2 и резултатите от изчисленията, получени по-горе, определяме коефициента на вариация,%, съгласно формулата (6.3):
Ако коефициентът на вариация надвишава 33%, това показва хетерогенността на изследваната популация. Получената стойност в нашия случай показва, че съвкупността от ученици по възраст е хомогенна по състав. По този начин важна функция на обобщаващите показатели за вариация е оценката на надеждността на средствата. По-малкотос1,а2 иV,колкото по-хомогенен е резултатният набор от явления и толкова по-достоверна е получената средна стойност. Според "правилото на трите сигми", разглеждано от математическата статистика, в нормално разпределени или близки до тях серии, отклонения от средната аритметична стойност, непревишаващи ± 3-та, се срещат в 997 случая от 1000. По този начин, знаейкиxи a, можете да получите обща първоначална представа за вариационните серии. Ако например средната заплата на служител в компанията е 25 000 рубли, а a е 100 рубли, тогава с вероятност, близка до сигурността, може да се твърди, че заплатата на служителите на компанията варира в рамките на (25 000 ± 3 x 100), т.е. от 24 700 до 25 300 рубли.